Die gleichung des kreises
Ein Kreis ist eine der bemerkenswertesten geometrischen Figuren.Es hat eine bemerkenswerte Symmetrie, die auf der Tatsache basiert, dass alle Punkte im Kreis gleichbleibig aus dem Zentrum sind, was in englischer Sprache bedeutet, dass alle Punkte im Kreis den gleichen Abstand von der Mitte sind.Diese gemeinsame Entfernung \(r\) wird als die genannt Radius des Kreises .
Der Kreis hat einige wichtige geometrische Anwendungen, die ihn sowohl in Geometrie als auch in Algebra ein wirklich wichtiges Objekt machen.
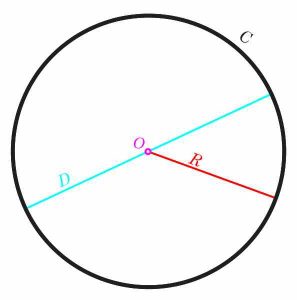
Eine weitere entscheidende Eigenschaft des Kreises ist, dass er sehr leicht algebraisch dargestellt wird.Dies bedeutet, dass wir leicht eine Gleichung festlegen können, um alle Punkte in einem bestimmten Kreis darzustellen.Betrachten Sie es konkreter, die Koordinatenebene \(X - Y\) zu betrachten.All dies bedeutet, dass wir die x- und y -Achsen haben, die senkrecht zueinander sind
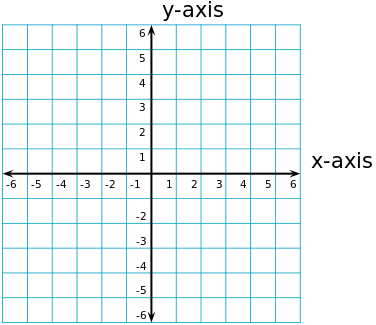
Kreisgleichung
Lassen Sie uns nun über die Gleichung sprechen, die alle Punkte eines bestimmten Kreises darstellt.In der Tat beschreibt die folgende Gleichung für einen Radiuskreis \(r\) Punkte \((x, y)\), die sich auf dem Kreis befinden:
\[\Large x^2 + y^2 = r^2\]Das obige entspricht der Gleichung eines Radiuskreises \(r\) mit in der Mitte in \((0,0)\), dem Ursprung der Koordinatenachsen.
Wenn der Radius \(r = 1\) ist, haben wir das, was genannt wird Einheitskreis .
Wenn Sie sich die obige Gleichung ansehen, ist die geometrische Interpretation, dass \(x\) und \(y\) die Seiten eines Dreiecks sind und \(r\) ist seine Hypotenuse,
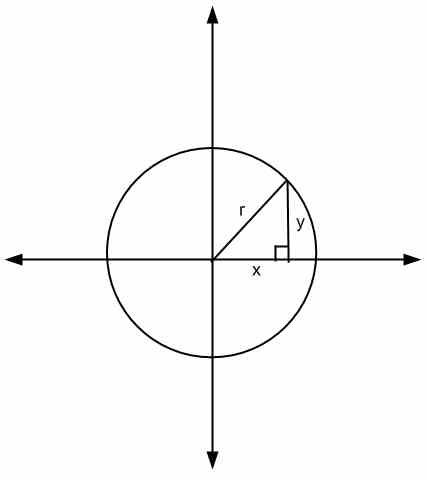
Eine andere Möglichkeit, die Gleichung des Kreises zu sehen, besteht darin, die Quadratwurzel auf beide Seiten der Gleichung zu übernehmen. Daher würden wir \(\sqrt{x^2+y^2} = r\) erhalten, was anzeigt Beruhnung Zumurprung (In diesem Fall ist die Mitte des Kreises gleich \(r\).
Gleichung eines kreises, der nicht am ursprung zentriert ist
Ein Vorteil der Arbeit an koordinierten Achsen besteht darin, dass die Punkte auf dem Kreis und das Zentrum sein können Lokalisiert in den Achsen und kann wie oben gezeigt durch eine Gleichung dargestellt werden.Im Allgemeinen muss die Mitte des Kreises nicht der Ursprung sein, es kann jeder Punkt \((x_0, y_0\) in den koordinierten Achsen sein, in diesem Fall wird die Gleichung des Kreises:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]das ist als die bekannt Allgemeine Gleichung Eines kise .Angenommen, Sie müssen die Gleichung eines Radiuskreises \(r = 4\) berechnen, das am Punkt zentriert ist \((1,2)\).In diesem Fall haben wir \(x_0 = 1\), \(y_0 = 2\) und \(r = 4\) und dann schließen wir diese Zahlen einfach in die obige Gleichung und wir bekommen
\[\large (x-1)^2 + (y-2)^2 = 4^2\]oder wir können auch schreiben
\[\large (x-1)^2 + (y-2)^2 = 16\]Beispiel 1
Schreiben Sie die Gleichung des Radius 3 mit der Mitte am Ursprung.Bestimmen Sie unter Verwendung der Gleichung, ob der Punkt (1, 2) zum Kreis gehört oder nicht.
Antworten:
Lassen Sie uns zunächst die Gleichung des Kreises bestimmen.In diesem Fall ist der Kreis am Ursprung zentriert, also \((x_0, y_0) = (0, 0)\).Daher ist die Gleichung
\[\large x^2 + y^2 = 3^2\]das ist das gleiche wie
\[\large x^2 + y^2 = 9\]Die Frage ist nun, ob sich der Punkt (1, 2) auf dem Kreis befindet oder nicht.Wir wissen, dass die Punkte im Kreis so werden, dass \(x^2 + y^2 = 9\).
Für den Punkt \((1, 2)\) erhalten wir das \(x = 1\) und \(y=2\), also für diesen Fall dieses Punktes \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\), der sich von 9 unterscheidet, und daher \((1,2)\)gehört nicht zum Kreis.
Mehr über die gleichung des kreises
Der Kreis ist eine so wichtige Mathematikeinheit, dass über ihn geschrieben wurde.Kreise überqueren Geometrie, Trigonometrie und Algebra. Deshalb ist es in der Mathematik überall ein transversales Erscheinungsbild.
Wie kann man die gleichung eines kreises ausarbeiten?
Wenn wir mit einem Kreis arbeiten, gibt es mehrere Dinge zu trainieren.Das erste ist, die Gleichung des Kreises zu konstruieren.Betrachten Sie beispielsweise einen Radiuskreis \(r = 3\), der am Punkt zentriert ist \((1,1)\).
Basierend auf der allgemeinen Gleichung eines Kreises ist die Gleichung
\[\large (x-1)^2 + (y-1)^2 = 3^2\]Die obige Gleichung kann beispielsweise verwendet werden, um festzustellen, ob ein Punkt zum Kreis gehört oder nicht.Was können Sie sonst noch tun, um die Gleichung des Kreises auszuarbeiten?Sie könnten möglicherweise die Quadrate erweitern, also bekommen wir
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]was vereinfacht werden kann in
\[\large x^2 - 2x + y^2 -2y = 7\]Beide Gleichungen sind also gleichwertig in dem Sinne, dass sie den gleichen Kreis bestimmen.Welches bevorzugen Sie?\((x-1)^2 + (y-1)^2 = 3^2\) oder \(x^2 - 2x + y^2 -2y = 7\)?Es ist eine Frage des Geschmacks und wofür würden Sie die Formel verwenden.
Kreisbereich
Interessanterweise, um das zu berechnen Kreisberich Sie brauchen nicht die vollständige Gleichung, Sie müssen nur den Radius kennen.Mit anderen Worten, die Bereich und Umfang ein Abhängig von seinem Zentrum nicht abhängig.
Ist die gleichung eines kreises eine funktion?
Dies ist eine Frage, die viele Schüler haben, und wir müssen klären.Zunächst die Kreisgleichung ist eine Gleichung, keine Beziehung oder Funktion.
Jetzt bestimmt die Gleichung des Kreises eine Beziehung und nicht a Funkwerk , wenn Sie algebraisch Lösen Sie für Bezug auf x .In der Tat, wenn wir für \(y\) lösen, bekommen wir:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]Das bedeutet, dass für eine gegebene \(x\) zwei Werte von \(y\) zugeordnet sind, die \(\sqrt{ 9 - x^2}\) und \(-\sqrt{ 9 - x^2}\) sind, was darauf hinweist, dass die Gleichung des Kreises a bestimmt aBeziehung statt einer Funktion.
Ein spezifischer Fall des Kreises ist der Einheitskreis mit Gleichung \(x^2 + y^2 = 1\) ist das auf den Ursprung zentriert.Der Einheitskreis ist besonders geeignet, mit denen er arbeiten kann Trigonometrische Austrücke auf sehr visuelle Weise.
