Mehr über die korrelationsmatrix

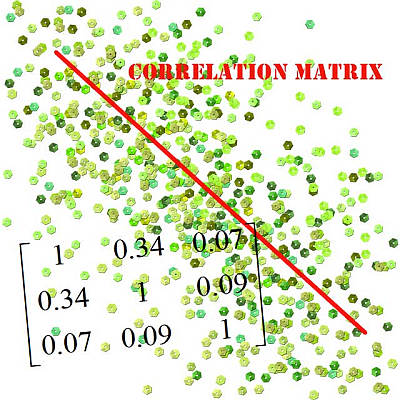
Eine Korrelationsmatrix ist eine Tabelle, in der die paarweisen Korrelationen zwischen mehreren Variablen in praktischer Weise in einer Matrixform organisiert sind. Der Wert in der i-ten Zeile und j-ten Spalte entspricht der Korrelation zwischen den Variablen \(X_i\) und \(X_j\).

Einfach ausgedrückt ist die Korrelationsmatrix eine Zusammenfassung aller Korrelationen, die für einen Satz von Variablen gefunden werden können, für die Stichprobendaten verfügbar sind.

Die Korrelationsberechnung ist von entscheidender Bedeutung, denn sie ist der vorherige Schritt zur Anwendung einer Linearer Regressionstrechner um das Modell der kleinsten Quadrate zu finden. Dies sollte jedoch nur versucht werden, wenn die die Korrelation wird als signifikant eingestuft .

Formel für die korrelationsmatrix

Da \(corr(X_i, X_j) = corr(X_j, X_i)\), dann ist die Korrelationsmatrix symmetrisch, und aus diesem Grund, um nicht redundant zu sein, berichtet die Korrelationsmatrix nur die Werte von der Diagonale und aufwärts. Für andere Korrelationsoperationen können Sie einen Korrelationskoeffizienten zu berechnen mit allen Schritten, oder Sie können Folgendes verwenden rechner für die kritische Korrelation .

Wie berechnet man eine korrelationsmatrix?

Um zu verstehen, wie man eine Korrelationsmatrix berechnet, muss man zunächst wissen, wie man die Pearsonsche Korrelation berechnet, denn die Korrelationsmatrix ist einfach die Matrix der Korrelationen zwischen allen möglichen Variablenpaaren.

Um mit der Berechnung der Korrelationsmatrix fortzufahren, müssen Sie die folgenden Schritte ausführen:

Schritt 1: Listen Sie die Variablen auf, die Sie haben, z. B. X1, X2, ..., usw. Jeder dieser Variablen ist eine Stichprobe zugeordnet

Schritt 2: Nehmen Sie die i-te und j-te Variable aus Ihrer Liste, Xi und Xj, und berechnen Sie den Korrelationskoeffizienten für sie. Nennen Sie ihn \(r_{ij}\)

Schritt 3: Nehmen Sie den Wert \(r_{ij}\) und das wird der Wert der Zeile i, Spalte j der Korrelationsmatrix

Korrelationswerte nahe bei 1 oder -1 deuten auf starke lineare Zusammenhänge hin, was bedeutet, dass ein Linearer Regressionstrechner (oder ein multiple lineare Regression je nachdem, wie viele Prädiktoren Sie haben).

Wie verwendet man eine korrelationsmatrix?

Dies ist ein Punkt, der angesprochen werden muss, da eine Korrelationsmatrix oft in verschiedenen Formaten angegeben werden kann. Die Korrelationsmatrix ist eine Tabelle mit der gleichen Anzahl von Zeilen und Spalten, wobei die Namen der Variablen in den entsprechenden Zeilen und Spalten erscheinen.

Wenn also die erste Variable \(X_1\) ist, dann gibt die erste Zeile den Korrelationskoeffizienten von \(X_1\) und jeder der anderen Variablen an. Und wenn die zweite Variable \(X_2\) ist, dann gibt die zweite Zeile den Korrelationskoeffizienten von \(X_2\) und jeder der anderen Variablen an, und so weiter.

Ausgehend von der Art und Weise, wie dies definiert ist, haben Sie in Zeile 1, Spalte 1 die Korrelation von \(X_1\) mit sich selbst, die 1 ist, dann haben Sie in Zeile 2, Spalte 2 die Korrelation von \(X_2\) mit sich selbst, die ebenfalls 1 ist, und so weiter.

Sie werden also feststellen, dass die Diagonale der Korrelationsmatrix immer nur 1en enthält. Da dies immer der Fall ist, wird in der berechneten Korrelationsmatrix oft die Diagonale weggelassen (denn wir wissen ja bereits, dass sie 1en enthält, warum sollte man sie also explizit angeben).

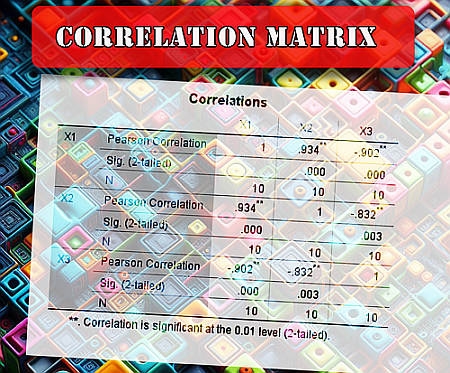
Aber es gibt noch etwas anderes zu beachten: Die Korrelation zwischen \(X_1\) und \(X_2\) ist die gleiche wie die Korrelation zwischen \(X_2\) und \(X_1\), also ist die Korrelationsmatrix symmetrisch die Werte unterhalb der Diagonale spiegeln also die Werte oberhalb der Diagonale wider.

Aus diesem Grund sieht man sehr oft eine Korrelationsmatrix, bei der nur die Werte oberhalb der Diagonale (oder darunter) angegeben werden, weil wir wissen, dass die Diagonale 1 ist und die Werte unterhalb der Diagonale ein Spiegelbild der Werte oberhalb der Diagonale sind.