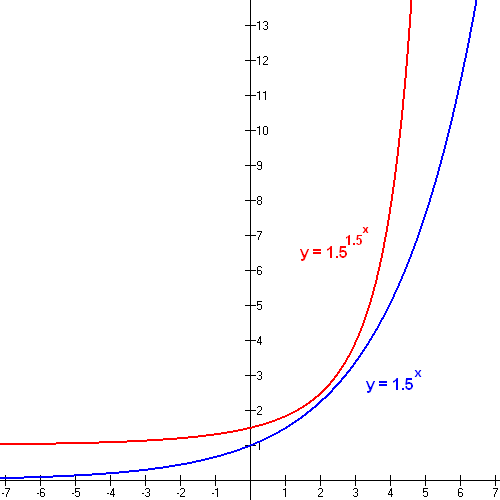
Rechner für exponentielles wachstum
Anweisungen: Verwenden Sie diesen Exponentialwachstumsrechner mit Schritten, um die Funktion zu finden, die das exponentielle Wachstum für die angegebenen Parameter beschreibt. Sie müssen den Anfangswert \(A_0\) und die Wachstumsrate pro Periode (jährlich oder kontinuierlich) angeben.
Der exponentialwachstums-rechner
Verwenden Sie diesen Exponentialwachstumsrechner, um eine Funktion zu spezifizieren, die wächst, indem Sie ihren Anfangswert und ihre Wachstums- (oder Zerfalls-)rate angeben. Um eine gültige Wachstumsrate zu erhalten, geben Sie eine positive Rate an.
Außerdem haben Sie die Möglichkeit zu entscheiden, wie diese Rate wirken soll, entweder jährlich oder kontinuierlich. Dann klicken Sie auf "Berechnen", um alle Schritte angezeigt zu bekommen.
Exponentielles Wachstum ist ein algebraisches Verhalten, das im wirklichen Leben viele Anwendungen hat, von Finanzen bis Wirtschaft, von Sozialwissenschaften bis Biologie. Es stellt ein Wachstum dar, das in jeder Periode mit einer bestimmten Rate (oder einem bestimmten Prozentsatz) aufgezinst wird.
Eine Sichtweise ist, dass die Änderungsrate ist proportional zur Größe der Funktion.
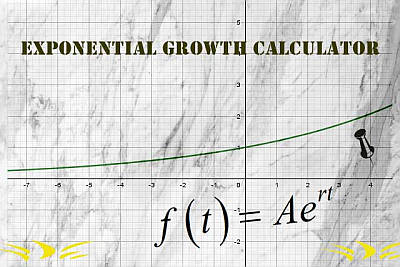
Exponentiale wachstumsformel
Man sagt, dass eine Funktion \(f(t)\) ein exponentielles Wachstumsverhalten hat, wenn sie als ausgedrückt werden kann:
\[f(t) = A_0 (1 + r)^t \]In der obigen Formel entspricht \(r\) der Wachstumsrate, ausgedrückt als Dezimalzahl oder als Prozentsatz (beide sind gleichwertig).
In der Regel werden Ihnen die Wachstumsrate und der Anfangswert \(A_0\) mitgeteilt, aber manchmal erhalten Sie auch Informationen über die Funktion, und Sie müssen die Parameter \(r\) und \(A_0\) ableiten.
Für die obige Formel für exponentielles Wachstum gibt es einen Sonderfall, in dem die Rate kontinuierlich aufgezinst wird; in diesem Fall lautet die Formel
\[f(t) = A_0 e^{rt} \]Typischerweise, exponentielles Wachstum funktionen stellen Geld dar, aber wie bereits erwähnt, können sie eine Vielzahl von Phänomenen darstellen, z. B. das Bevölkerungswachstum.
Diese Art von Phänomenen spiegelt sich in der Exponentialkurve wider, die zunächst relativ flach verläuft, dann aber rasch ansteigt.
Exponenzielles wachstum anwendungen
Sie können dies verwenden Exponentialfunktion -Wiederaufnahme für verschiedene Arten von Modellen, vorausgesetzt, Sie kennen die erforderlichen Parameter.
Ein typisches solches Modell betrifft bestimmte Populationen, die schnell wachsen. Dies kann bei Bakterien, Insekten und sogar menschlichen Populationen der Fall sein. Wenn Populationen schnell wachsen, wird der Wettbewerb um die Ressourcen in der Regel immer härter und das Wachstum hört auf, exponentiell zu sein.
Beachten Sie, dass dieser Rechner Ihnen auch den Graphen der resultierenden Exponentialfunktion anzeigt.
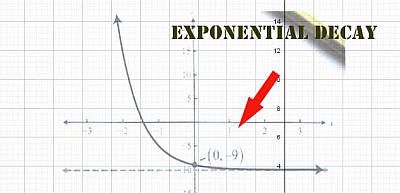
Wie hängen exponentialwachstum und exponentialzerfall zusammen?
Exponentielles Wachstum und exponentieller Zerfall sind absolut analog, und der Hauptunterschied besteht darin, dass die Rate \(r\) bei exponentiellem Wachstum positiv ist, während sie bei exponentiellem Zerfall negativ ist.
Sie können auch Folgendes verwenden Exponential -Zerfall -Rechner für das umgekehrte, aber analoge exponentielle Verhalten, das dem exponentiellen Zerfall entspricht, wobei die Wachstumsrate nun negativ ist.
Woher weiß ich also, ob es sich um Wachstum oder Verfall handelt? Ganz einfach, man schaut sich die Rate an. Wenn sie positiv ist, liegt Wachstum vor, wenn sie negativ ist, liegt Verfall vor.
Der Rechner für exponentielles Wachstum und exponentiellen Zerfall zeigt Ihnen alle Schritte an, die im Wesentlichen darin bestehen, zwei simultane Gleichungen mit zwei Unbekannten zu lösen
.Exponentiales wachstum von zwei punkten aus
Sie möchten jetzt vielleicht eine Exponentialfunktion berechnen von zwei Punkten aus, von denen bekannt ist, dass sie durchlaufen werden.
Aber wie findet man die exponentielle Wachstumsrate mit zwei Punkten? Man beginnt mit einer allgemeinen Exponentialgleichung der Form \(f(t) = A_0 e^{r t}\). Diese Gleichung hat zwei Unbekannte, nämlich \(A_0\) und \(k\).
Wenn man also zwei Punkte \((t_1, y_1)\) und \((t_2, y_2)\) in \(f(t) = A_0 e^{r t}\) einsetzt, erhält man zwei Gleichungen mit zwei Unbekannten, die lösbar sind, vorausgesetzt, dass \(t_1 \ne t_2\), was sinnvoll ist, weil wir nicht zwei Punkte mit der gleichen x-Koordinate haben wollen.