Binomialwahrscheinlichkeitsrechner

Mehr über die Binomialverteilungswahrscheinlichkeit so können Sie diesen Binomialrechner besser verwenden: Die Binomialwahrscheinlichkeit ist eine Art von diskreter Wahrscheinlichkeitsverteilung, die Zufallswerte im Bereich von \([0, n]\) annehmen kann, wobei \(n\) der Stichprobenumfang ist.

Eigenschaften der binomialwahrscheinlichkeit

Die Haupteigenschaften der Binomialverteilung sind:

• Es ist diskret und kann Werte von 0 bis n annehmen, wobei n die Stichprobengröße ist


• Die Art der Schiefe hängt von den Parametern n und p ab


• Es wird durch zwei Parameter bestimmt: den Bevölkerungsanteil des Erfolgs P, die Stichprobengröße n (oder die Anzahl der Versuche)


• Das Mittelwert der Binomialverteilung ist \(n\cdot p\) und seine Standardabweichung ist \(\sqrt{np(1-p)}\)

Was ist die binomialwahrscheinlichkeitsformel?

Die Formel, die die Binomialwahrscheinlichkeit definiert (die als ihre bezeichnet wird Wahrscheinlichkeitsverteilungsfunktion ) ist:

\[\Pr(X = k) = \left( \begin{matrix} n \\\\ k \end{matrix} p^k \cdot (1-p)^{n-k} \]

wobei n und p die entsprechenden Parameter der Verteilung sind. Das heißt, n ist die Anzahl der Versuche und p ist die Erfolgswahrscheinlichkeit der einzelnen Versuche.

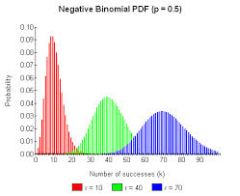
So verwenden sie diesen binomialverteilungsrechner mit schritten

Verwenden der oben genannten Binomialverteilungskurvenrechner sind wir in der Lage, Wahrscheinlichkeiten der Form \(Pr(a \le X \le b)\), der Form \(\Pr(X \le b)\) oder der Form \(\Pr(X \ge a)\) zu berechnen. Jede andere Art von Ereignis lässt sich aus diesen elementaren Ereignistypen ableiten.

Sie möchten zum Beispiel die Wahrscheinlichkeit ermitteln, dass X zwischen 0 und 1 oder zwischen 3 und 4 liegt. Diese Wahrscheinlichkeit würden Sie als \( \Pr(0 \le X \le 1) + \Pr(3 \le X \le 4)\) berechnen

Geben Sie die entsprechenden Parameter für \(n\) und \(p\) in das obige Textfeld ein, wählen Sie die Art der Schwänze, geben Sie Ihr Ereignis an und berechnen Sie Ihre Binomialwahrscheinlichkeit, wobei alle Details der Binomialwahrscheinlichkeitsformel Schritt für Schritt angezeigt werden.

Andere wichtige wahrscheinlichkeitsverteilungsrechner

Die Binomialverteilung ist eine Art diskrete Verteilung.Andere Taschenrechner für diskrete Verteilungen sind unsere Poisson -Veilungsrechner , Hyper-Geometrischer Taschenrechner oder unsere Geometrische Vertelungsrechner .

Was passiert, wenn die erfolgswahrscheinlichkeit nicht konstant ist?

Eine verallgemeinerte Form des Binomialkoeffizienten ist die Multinomialkoeffizient die Kombinationen von \(k\) Zahlen, die sich zu \(n\) addieren, mit \(k \ge 2\) berücksichtigt.

Wenn Sie nun mit einer kontinuierlichen Verteilung zu tun haben, möchten Sie möglicherweise unsere überprüfen NORMALER TEHRSCHEINLICHKEITSRECHNER ONLINE , die sich mit der Normalverteilung und verwandten Ereignissen befasst, die die häufigste kontinuierliche Verteilung ist.

Beispiel: berechnung von binomialwahrscheinlichkeiten

Frages : Nehmen wir an, dass X eine Zufallsvariable mit einer Binomialverteilung mit den Parametern n = 10 und p = 0,45 ist. Berechnen Sie \(\Pr(2\le X\le 4)\).

Lösung:

Wir müssen eine Binomialverteilungswahrscheinlichkeit berechnen.Die folgenden Informationen werden bereitgestellt:

Population Probability of Success \((p)\) =	\(0.45\)
Sample Size \((n)\) =	\(10\)
Probability Event =	\(\Pr(2 \leq X \leq 4) \)

Dies impliziert das

\[\Pr(2 \le X \le 4) = \Pr(X = 2) + \Pr(X = 3) + \Pr(X = 4)\]\[= \left( \begin{matrix} 10 \\\\ 2 \end{matrix}\right) 0.45^{ 2} \cdot 0.55^{ 10-2} + \left( \begin{matrix} 10 \\\\ 3 \end{matrix}\right) 0.45^{ 3} \cdot 0.55^{ 10-3} + \left( \begin{matrix} 10 \\\\ 4 \end{matrix}\right) 0.45^{ 4} \cdot 0.55^{ 10-4}\]\[= 0.0763 + 0.1665 + 0.2384\] \[= 0.4811\]

was bedeutet, dass die gesuchte Wahrscheinlichkeit \(\Pr(2 \leq X \leq 4) = 0.4811 \) ist.