Usando a regra de sinais de descartes

Esta calculadora irá ajudá-lo com a aplicação da Regra de Sinais de Descartes, para qualquer polinômio que você fornecer. O único requisito para isso é que o polinômio seja válido.

Por exemplo, você pode fornecer um polinômio cúbico simples como x^3 - 2x + 1, mas também pode fornecer um mais complicado, como x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^ 2 + 2x + 1, etc.

Depois de fornecer um válido função polinomial , você clica no botão "Calcular", a fim de obter todas as etapas do processo mostradas.

Encontrando zeros polinomiais é uma das tarefas mais importantes em álgebra, mas não é uma tarefa fácil em geral. Não há fórmulas gerais para todos os polinômios de todos os graus, então geralmente temos que seguir um procedimento sistemático para encontrar o maior número possível de raízes.

Nesse contexto, ter o máximo de informações disponíveis sobre o tipo de raízes é sempre útil, e esse é um dos objetivos da Regra dos Signos de Descartes.

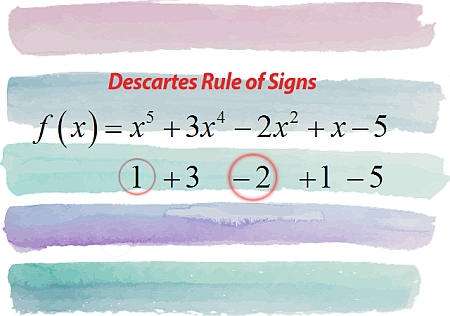
O que afirma a regra dos sinais de descartes?

Em termos simples, a Regra dos Sinais de Descartes diz algo sobre o número de raízes positivas e negativas de um polinômio, apenas observando os sinais dos coeficientes do polinômio dado.

Mais precisamente, você começa com o coeficiente líder e ignora os coeficientes zero e vai contando as mudanças no sinal. O número total de mudanças no sinal de coeficientes consecutivos é um limite superior para o número de raízes positivas de \(p(x)\), e o número de raízes positivas tem a mesma paridade que o número total de mudanças nos sinais.

Então, você faz o mesmo exercício, mas para os coeficientes de \(p(-x)\), e o que você obtém nesse caso é que o número total de mudanças no sinal de coeficientes consecutivos é um limite superior para o número de raízes negativas de < >, e o número de raízes negativas tem a mesma paridade que o número total de mudanças de sinal.

Etapas para aplicar a regra de sinais de descartes

• Passo 1: Identifique o polinômio p(x) que você precisa analisar. Certifique-se de que é um polinômio (caso contrário, o método não funciona) e simplifique-o o máximo possível
• Passo 2: Coloque os coeficientes de p(x) em uma linha, começando pelo coeficiente líder, em ordem decrescente e omitindo os coeficientes zero
• Passo 3: Começando pelo coeficiente líder, conte as mudanças de sinal entre coeficientes consecutivos, anote o número total de mudanças de sinal e chame-o de T
• Passo 4: O número de zeros positivos de p(x) é no máximo T e tem a mesma paridade que T (se T é par, então o número de zeros positivos de p(x) é um número par, e se T é ímpar, então o número de zeros positivos de p(x) é um número ímpar)
• Passo 4: Repita o mesmo processo agora para os coeficientes de p(-x), para obter informações sobre o número de zeros negativos de p(x)

Este método pode fornecer a você potencialmente uma gama de valores possíveis para o número de zeros positivos (e negativos), mas também pode dizer EXATAMENTE quantos zeros positivos (ou negativos) um determinado polinômio tem, dependendo apenas de quantas mudanças de sinal você conta.

Posso calcular os zeros reais com este método?

Não, a Regra de Sinais de Descartes não pretende fornecer informações sobre quais são as raízes reais, apenas informa algo sobre o NÚMERO de raízes positivas (e negativas).

Agora, combinando essas informações, com o teorema da raiz racional e outras ferramentas elementares, incluindo Divisão Sintética e a teorema do fator , você estará mais bem equipado para observar o valor real das raízes.

Dicas e truques

Sempre simplificar o polinômio primeiro. Por exemplo, se você tem \(p(x) = x^5 - x^3\), você vai querer primeiro para \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\), então você sabe que 0 é uma raiz (com multiplicidade 3), e você aplica a regra de Descartes para \(x^2 - 1\) em vez de.

Exemplo: regra dos sinais de descartes

Indique o número possível de raízes positivas e negativas de \(x^4 - x^3 + x^2 + 1\)

Solução: Temos a seguinte função polinomial: \(\displaystyle x^4 - x^3 + x^2 + 1\), para a qual precisamos aplicar a Regra de Sinais de Descartes.

Raízes Positivas : Os coeficientes polinomiais (da maior para a menor potência) são:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

Descobrimos que o número de mudanças de sinal em coeficientes consecutivos é: \(2\), e as mudanças são: \(\,\,+1\,\,\) e \(\,\,-1\,\,\), \(\,\,-1\,\,\) e \(\,\,+1\,\,\).

Raízes Negativas : Os coeficientes polinomiais para \(p(-x) = x^4+x^3+x^2+1\) são:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

Nenhuma mudança de sinal foi encontrada para os coeficientes de \(p(-x)\).

Conclusão: Com base no número de mudanças de sinal encontrado, que é \(2\), concluímos que \(p(x)\) pode ter 0 ou 2 raízes positivas para \(p(x) = x^4-x^3+x^2+1\).

Agora, como não foram encontradas mudanças de sinal para os coeficientes de \(p(-x)\), concluímos que NÃO há zeros negativos para \(p(x) = x^4-x^3+x^2+1\).

Exemplo: mais da regra do sinal de descartes

Indique o número possível de raízes positivas e negativas de \(x^4 + x^3 + x^2 - 1\)

Solução: Agora precisamos analisar \(\displaystyle x^4 + x^3 + x^2 - 1\), com a Regra de Sinais de Descartes.

A expressão fornecida já está simplificada, então não há mais nada para simplificar.

Raízes Positivas : Os coeficientes são:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Observe que o número de mudanças de sinal em coeficientes consecutivos neste caso é igual a \(1\), e as mudanças são: \(\,\,+1\,\,\) e \(\,\,-1\,\,\).

Raízes Negativas : Os coeficientes polinomiais associados a \(p(-x) = x^4-x^3+x^2-1\) são:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Então, o número de mudanças de sinal em coeficientes consecutivos é igual a \(3\), e as mudanças são: \(\,\,+1\,\,\) e \(\,\,-1\,\,\), \(\,\,-1\,\,\) e \(\,\,+1\,\,\), \(\,\,+1\,\,\) e \(\,\,-1\,\,\)

Conclusão: Como há uma mudança de sinal entre os coeficientes de \(p(x)\), concluímos que há exatamente UM zero positivo para \(p(x) = x^4+x^3+x^2-1\).

Com base no número de mudanças de sinal encontrado, que é \(3\), concluímos que \(p(x) = x^4+x^3+x^2-1\) pode ter 1 ou 3 raízes negativas.

Exemplo: sinais positivos e negativos

Indique o número possível de raízes positivas e negativas de \(x^4 + 1\). Você pode dizer algo sobre o número exato de raízes positivas e negativas?

Solução: Neste caso não há mudanças de sinal, então não há raízes positivas. Agora, \(p(-x) = (-x)^4 + 1 = x^4 + 1\), que não tem mudança de sinal, então também não há raízes negativas. A conclusão é que o polinômio não possui raízes reais (já que 0 também não é raiz).

Mais calculadoras polinomiais

Encontrando raízes polinomiais é um dos pontos centrais para a maioria dos problemas de aplicação em Cálculo e Álgebra, e é uma habilidade que vale a pena dominar.

Existem muitas habilidades envolvidas no cálculo de zeros de um polinômio, e Regra Dos Sinais De Descartes fornece muitas informações que podem ser inferidas simplesmente observando os coeficientes do polinômio.