Mais sobre o modelo log-log

Esta calculadora permitirá que você calcule um modelo de regressão log-log para dados que você fornecer. Esses dados precisam de um reflexo adequado de um modelo log-log, no qual precisa haver um grau linear razoável de associação entre ln(X) e ln(Y).

Depois de fornecer dados válidos, que neste caso significam dados positivos para X e Y, você terá que clicar no botão "Calcular" para começar e poder ver todas as etapas do processo.

O modelo log-log tem fortes aplicações práticas, especialmente no campo da Economia, em que é usado para calcular elasticidades .

O que é o modelo log-log?

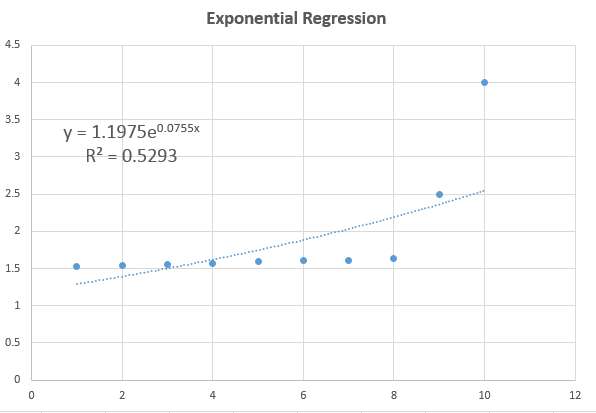
O modelo log-log, como o nome pode sugerir, é um modelo no qual \(\ln(X)\) exibe um grau significativo de associação linear com \(\ln(Y)\). Com base neste fato, se tornar apropriado calcular um modelo de regressão para esses dados de transformação, então procuramos os coeficientes de regressão \(a\) e \(b\) para estimar

\[\displaystyle \ln(Y) = a + b \ln(X)\]

Então, uma calculadora de um modelo log-log se reduz a um cálculo de um modelo de regressão regular para os dados transformados \(\ln(X)\) e \(\ln(Y)\).

Etapas para estimar um modelo log-log

• Passo 1: Identifique claramente as variáveis X e Y. Certifique-se de que elas tenham o mesmo tamanho de amostra e que AMBAS sejam positivas, caso contrário, você não poderá executar um modelo log-log
• Passo 2: Transforme os dados originais X e Y nos auxiliares ln(X) e ln(x)
• Etapa 3: Use uma equação de modelo de regressão regular, onde você calcula o declive e interceptação y para seus dados transformados em log ln(X) e ln(Y)

Depois de estimar os coeficientes de regressão correspondentes, você pode escrever a equação \(\displaystyle \ln(Y) = a + b \ln(X)\), que pode deixar como está ou transformá-la como:

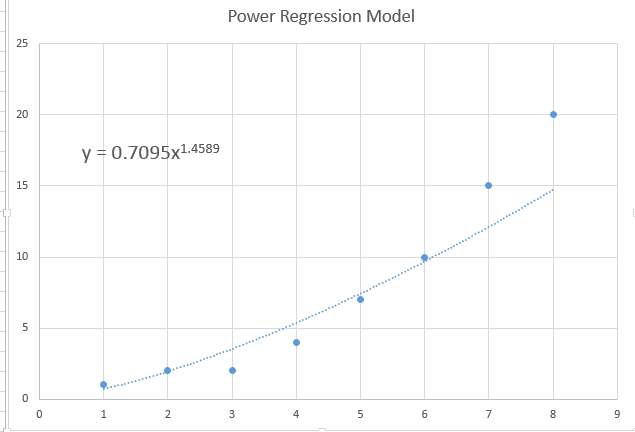
\[\displaystyle Y = e^a \cdot x^b \]

Interpretação do modelo log-log

Como podemos interpretar os coeficientes encontrados de uma forma como fizemos com a regressão usual de um ponto de vista de mudança marginal? Para um problema de regressão típico, você tem o coeficiente de inclinação que pode ser interpretado como o aumento médio na variável Y quando a variável X é aumentada em uma unidade.

Em um modelo log-log, não funciona bem assim, mas tem uma interpretação marginal similar. Na verdade, em um modelo \(\displaystyle \ln(Y) = a + b \ln(X)\), podemos interpretá-lo da seguinte forma:

Um aumento de 1% em X traz um aumento médio em Y de b% . Naturalmente, se \(b\), isso corresponde a uma diminuição.

Por que usamos esse tipo de modelo

Uma razão muito poderosa é que ela tem forte aplicação em Economia. A ideia de que a elasticidade-preço da demanda é simplesmente encontrada ao calcular o coeficiente de inclinação de um modelo log-log a torna relevante o suficiente para considerá-la.

Além disso, a ideia de uma mudança marginal relativa tem muitas outras aplicações na Teoria da Utilidade em Economia, tornando-a um modelo extremamente prático e aplicável.

Exemplo de cálculo de regressão log-log

Considere os seguintes dados para X e Y:

X: 1, 2, 3, 4, 5, 6, 7

Y: 10, 11,1, 13, 15,6, 16,8, 20, 22,4

Estime o modelo log-log correspondente e apresente um gráfico de dispersão adequado

Solução:

que conclui o cálculo.

Mais calculadoras de regressão

Você precisará avaliar se tem um coeficiente de correlação significativo entre ln(X) e ln(Y) antes de executar o modelo. Também é uma boa ideia faça um gráfico de dispersão dos dados para ver se são consistentes com o que se espera de uma associação log-log.

Muitas vezes, há apenas um nível sutil de curvatura, e os dados mostrarão um padrão quase plano, o que também é consistente com um modelo de regressão tradicional, mas também pode ser um modelo de regressão de potência com coeficientes muito pequenos.