Saiba mais sobre esta calculadora com passos.

O y-intercepção de uma linha é o ponto onde a linha atravessa o eixo \(y\)-, e é um ponto muito relevante em muitos contextos.

Para utilizar esta calculadora é necessário utilizar os seguintes passos:

1. Seleccione uma forma de definir a linha. Pode realmente fornecer uma equação da linha fornecer dois pontos da linha, ou um ponto da linha e a inclinação
2. Certifique-se que escolhe pelo menos um dos métodos e forneça as informações necessárias para a opção seleccionada
3. Clique em "Calcular"

Como se calcula o y-intercepção?

A forma como se calcula o y-intercepção dependerá de como se especificou a linha. Muitas vezes, é possível observar o gráfico da linha e mais ou menos estimar onde ela atravessa o eixo y, que é o encontrar o y-intercepção sobre o método gráfico .

Dessa forma poderá então ter uma ideia, pelo menos, do valor aproximado do y-intercepção

Como encontrar y-intercepção com a encosta?

A forma ideal, no entanto, é calcular algébricamente o y-intercepção. Por exemplo, quando se tem o equação em forma de intercepção em declive, utilizando a fórmula da linha.

\[y = mx + n\]

já se sabe que o y-intercepção é <\(n\)>. Porquê? porque <\(y\), em função de \(x\) é \(y = mx + n\)>>. Então, quando x = 0, obtemos \(y = n\), e sabemos \(x = 0\)> é o ponto em que o gráfico cruza o eixo y

O conceito y é um número ou um par (x, y)?

Depende um pouco da convenção que se utiliza. Se o valor y em que a linha cruza o eixo y é \(y_{intercept}\), então a forma mais comummente utilizada é que o intercepção y é o par \((0, y_{intercept})\)>>.

No entanto, se disser que o conceito y é apenas \(y_{intercept}\), isso também é correcto, apenas que alguns instrutores lhe irão pedir para escrever o conceito y como um par ordenado.

Mas a coordenada x do conceito y é SEMPRE 0, pelo que algumas pessoas consideram redundante escrever o par completo.

Posso obter a calculadora y-interceptora a partir de dois pontos?

Sim. Nesse caso, é necessário utilizar primeiro o dois pontos para encontrar a encosta utilizando a seguinte fórmula

\[m = \frac{y_2 - y_1}{x_2 - x_1} \]

Assim que tiver a inclinação, pode construir a forma de inclinação pontual usando

\[y - y_1= m (x -x_1)\]

E depois, resolvendo por \(y\), obterá o forma de intercepção de encostas o que lhe dá directamente o y-intercepção

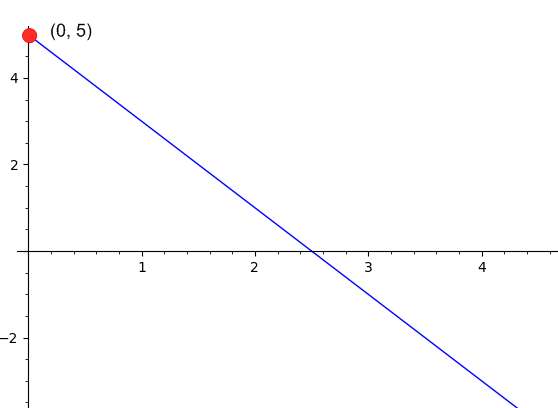
Exemplo: cálculo do conceito em y dadas duas linhas

Sabe-se que uma linha passa pelos pontos <\(\left(\displaystyle \frac{1}{4}, 1\right)\) e \(\left(\displaystyle \frac{15}{2}, 6\right)\)>>. Encontre o y-intercepção da linha.

Solução: : Cálculo do y-intercepção da linha

A informação fornecida sobre a linha é que a linha passa através dos pontos\(\displaystyle \left( \frac{1}{4}, 1\right)\) e \(\displaystyle \left( \frac{15}{2}, 6\right)\)>>

Por conseguinte, o primeiro passo consiste em calcular a inclinação. A fórmula para o declive é: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Agora, ao ligar os números correspondentes é , obtemos que a inclinação é: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 6 - 1}{ \displaystyle \frac{15}{2} - \frac{1}{4}} = \frac{ \displaystyle 6-1}{ \displaystyle \frac{15}{2}-\frac{1}{4}} = \frac{20}{29}\]

Então, agora sabemos que a inclinação é \(\displaystyle m = \frac{20}{29}\) e que a linha passa pelo ponto \(\displaystyle \left( \frac{1}{4}, 1\right)\)>

Assim, com a informação de que dispomos, podemos construir directamente a forma pontiaguda da linha, que é

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]>>

e depois ligando os valores conhecidos de <\(\displaystyle b = \frac{20}{29}\) e \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{4}, 1\right)\), obtemos que

\[\displaystyle y-1 = \frac{20}{29} \left(x-\frac{1}{4}\right)\]>>

Agora, precisamos de expandir o lado direito da equação, distribuindo a inclinação, de modo a obter \[\displaystyle y = \frac{20}{29} x + \frac{20}{29} \left(-\frac{1}{4}\right) + 1\]>

e simplificando, vamos obter que <\[\displaystyle y=\frac{20}{29}x+\frac{24}{29}\]>>>

Conclusão : Com base nos dados fornecidos, concluímos que a linha atravessa o eixo y a \(\displaystyle y = \frac{24}{29}\), portanto, o ponto de intercepção y correspondente é \(\displaystyle \left(0, \frac{24}{29}\right)\)>>.

Outro cálculo que também lhe pode interessar é aquele que utiliza o nosso calculadora de intercepção x que é o ponto em que a linha atravessa o eixo x.

As interceptações de uma linha fornecem uma excelente intuição gráfica do que a linha está a fazer, e têm aplicações directas quando resolução de sistemas de equações , ou em economia quando se calcula os excedentes de consumidores e produtores.