Derivadas trigonométricas inversas

Com esta calculadora você poderá calcular derivadas de funções trigonométricas inversas, mostrando todas as etapas do processo.

A ideia é que a função que você fornece contém uma função trigonométrica inversa, por exemplo f(x) = x^2/arctan(x+1), apenas para dar um exemplo.

Quando estiver pronto e terminar de digitar a função que você precisa diferenciar, clique no botão "Calcular" para ver todas as etapas do processo e cálculos.

A ideia de calculando derivativos das funções trigonométricas inversas é natural, e veremos nos próximos parágrafos que elas podem ser derivadas diretamente da derivadas trigonométricas que você sabe.

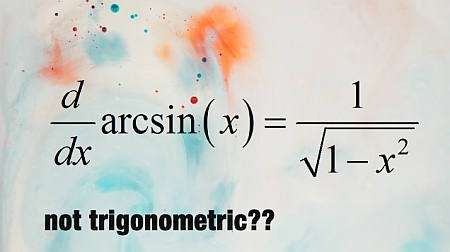
Funções trig inversas

Em termos simples, a função trigonométrica inversa são aquelas funções que ao avaliá-las na função trigonométrica correspondente, levam à identidade. Por exemplo, se considerarmos a função $\sin(x)$, sua função inversa é $\arcsin(x)$, e esta inversa tem a propriedade de

$$\sin(\arcsin(x)) = x$$

assim como

$$\arcsin(\sin(x)) = x$$

para todo $x$ em um determinado intervalo. Então, estritamente, $\arcsin(x)$ é a função inversa de $\sin(x)$ de um ponto de vista algébrico. E o mesmo vale para as outras funções trigonométricas inversas e suas funções trigonométricas correspondentes.

Cálculo de derivadas trigonométricas inversas

Então, se $f$ é uma função, e tem um inverso $f^{-1}$, então temos que

$$f^{-1}(f(x)) = x$$

para todos os $x$. Então, se diferenciarmos os dois lados da igualdade e usarmos a Regra da Cadeia no lado esquerdo, obtemos

$$\displaystyle (f^{-1})'(f(x))f'(x) = 1$$ $$\displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}$$

Agora, se definirmos $y = f(x)$, então $x = f^{-1}(y)$, o que leva a

$$\displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}$$ $$\Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}$$

Como usamos isso para funções trigonométricas inversas? Assuma $f(x) = \sin(x)$ e $f^{-1}(x) = \arcsin(x)$. Então, de acordo com a relação geral entre a derivada de uma função e a derivada de sua inversa, obtemos

$$\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}$$ $$\Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}$$

Mas um bom truque geométrico nos diz que

$$\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2}$$

o que implica que

$$\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}$$

O restante das derivadas trigonométricas inversas são obtidas com argumentos semelhantes.

Quais são as 6 funções trigonométricas inversas básicas?

• #1: $\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}$>
• #2: $\displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}$>
• #3: $\displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}$>
• #4: $\displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}$>
• #5: $\displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}$>
• #6: $\displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}$>

Curiosamente, ao calcular a derivada de funções trigonométricas inversas, nenhuma das derivadas trigonométricas inversas envolve funções trigonométricas ou funções trigonométricas inversas.

Aplicações da derivada de funções trigonométricas inversas

Funções trigonométricas e suas derivadas, bem como funções trigonométricas inversas e suas derivadas fazem parte do inventário de funções e operações básicas, usadas como blocos de construção, para criar funções mais complicadas.

Embora as funções trigonométricas apareçam com mais frequência nas aplicações do que as funções trigonométricas inversas, as últimas também têm um lugar claro no Cálculo, especialmente ao diferenciar e usar o método de decomposição de frações parciais.

Dicas e truques

Não se esqueça que as derivadas das funções trigonométricas inversas podem ser extremamente úteis, especialmente ao integrar termos que possuem um denominador quadrático.

Além disso, é fácil cometer erros ao calcular derivadas trigonométricas inversas por definição, você definitivamente pode se beneficiar usando um calculadora derivada que mostrará as etapas ou que você pode usar para verificar seu trabalho.

Exemplo: derivadas trig inversas

Calcule a derivada de: $f(x) = x + \arcsin(x^2)$

Solução: Para este primeiro exemplo, vamos analisar $\displaystyle f(x)=x+\arcsin\left(x^2\right)$. Esta função envolve uma função trigonométrica inversa, combinada com outra função. Vamos calcular sua derivada:

Respondente : Podemos concluir que a derivada da função é:

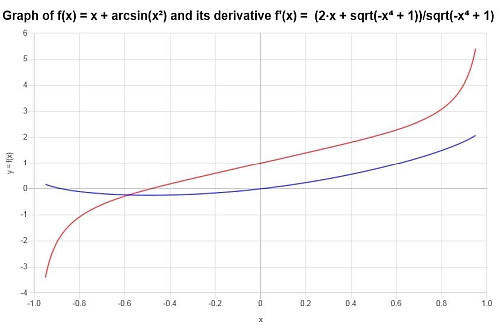
$$f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}$$

Podemos ver tanto a função quanto sua derivada no seguinte gráfico:

Exemplo: mais derivadas trigonométricas inversas

Considere a seguinte função: $f(x) = \frac{\arcsin(x)}{x}$, calcule sua derivada.

Solução: Já para o segundo exemplo, temos a função $\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}$.

Conclusão Final : A derivada que estamos procurando é:

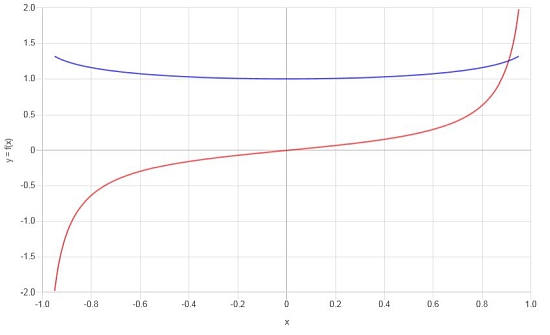
$$f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}$$

Graficamente, temos o seguinte:

Exemplo de derivadas trigonométricas inversas

Calcule a derivada de: $f(x) = x \arctan(x+1)$

Solução: Já para este exemplo final, trabalharemos com a função $\displaystyle f(x)=x\arctan\left(x+1\right)$, que contém uma função inversa.

Conclusão : Depois de simplificar, a derivada é:

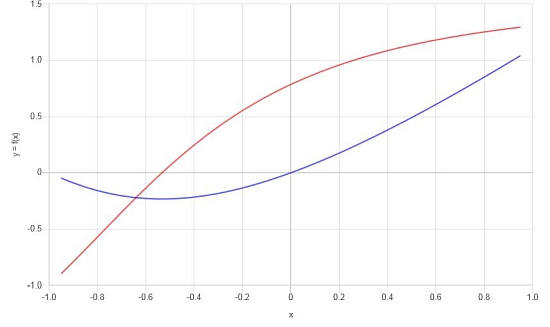
$$f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}$$

Com base nos resultados encontrados, podemos construir o seguinte gráfico para f e f':

Outras calculadoras de cálculo

ao usar derivadas trigonométricas , afirmamos que eles eram blocos de construção cruciais para a aplicação básica Regras de Derivadas .

Derivadas para funções trigonométricas inversas podem ser derivadas simplesmente da Derivativos de derivadas trigonométricas básicas, e é por isso que também as consideramos dentro do grupo de derivadas básicas para aprender ou mesmo memorizar.