Mais sobre esta calculadora de gráfico cos

Esta calculadora permitirá que você gere o gráfico para qualquer função cosseno, junto com o amplitude, período e frequência , mostrando todas as etapas. Você precisa fornecer uma função válida envolvendo a função cosseno. Pode ser algo trivial como cos(x), ou você pode torná-lo mais complicado como 2*cos(1/3 x + pi) - 4/5.

Depois de fornecer uma função válida envolvendo cosseno, basta clicar em "Calcular" para obter os resultados e todas as etapas do processo mostradas.

cosseno é um função trigonométrica que tem uma infinidade de aplicações em matemática e física. É muito comumente usado também em Geometria, quando resolver triângulos .

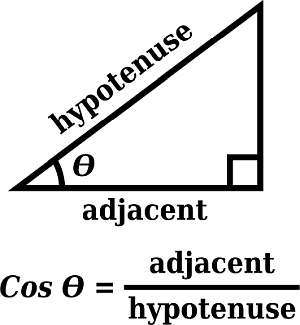
Como fazer um gráfico de cos?

O princípio principal ao representar graficamente qualquer tipo de função é recorrer a uma função simples conhecida para a qual conhecemos seu gráfico e, em seguida, construir o gráfico que queremos encontrar com base nas traduções e reescalonamento desse gráfico simples.

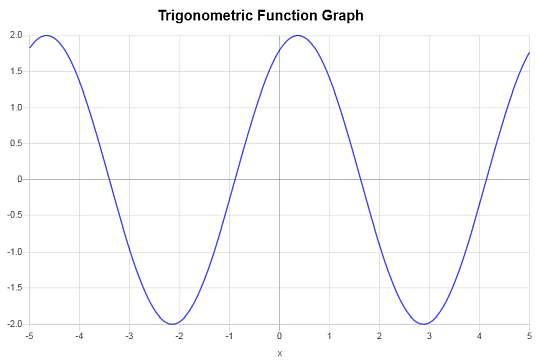
Para o caso do gráfico cos, sabemos que a expressão mais simples de uma função cosseno é f(x) = cos(x), que possui um gráfico que é mostrado abaixo:

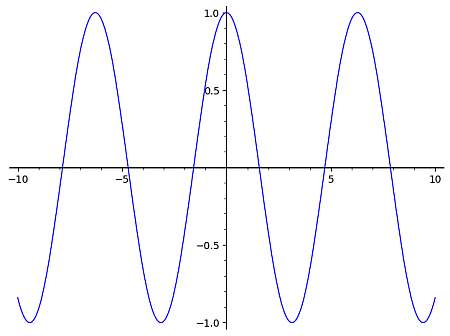
Então, podemos usar este gráfico base para derivar o gráfico de funções cos mais complexas, pois a forma geral será a mesma, apenas que pode ser potencialmente transladada para a esquerda ou para a direita, para baixo ou para cima, e o período também pode mudar, dependendo da função fornecida.

Quais são as etapas para representar graficamente uma função cosseno?

• Passo 1 : Identifique a função cos que deseja representar graficamente na forma a*cos(bx+c)+d, se possível
• Passo 2 : O valor de a corresponderá ao amplitude , d são as unidades em que o gráfico de cos básico é transladado para cima e o gráfico é deslocado -c/b para a direita
• Estágio 3 : Se a função cos não estiver na forma a*cos(bx+c)+d, crie uma tabela de valores para x e f(x) (onde f(x) é a função cos fornecida) e calcule várias pontos que você pode usar para traçar manualmente a forma do gráfico cos

De fato, apenas as funções da forma a*cos(bx+c)+d terão uma expressão clara para amplitude, período, frequência e translações, mas não são as únicas funções de cosseno que você pode conceber. Por exemplo, \(f(x) = cos(x^2)\) é uma função cos, mas não possui período ou frequência, por exemplo.

Gráfico de cos versus gráfico de seno?

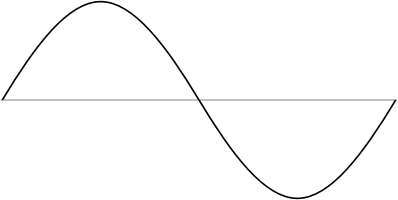
Quão semelhantes são os gráficos de cosseno e seno? Bom, bem parecido. Primeiro, observe que estamos falando sobre o gráfico básico de cos e gráfico de seno, isto é, sen(x) e cos(x).

Então, o gráfico do cos é obtido simplesmente deslocando o gráfico do seno para a esquerda \(\pi/2\) unidades. Portanto, o gráfico de cos e o gráfico de seno são essencialmente os mesmos, exceto por uma translação.

Gráfico de cos em graus

Existe alguma diferença entre o gráfico de cosseno em radianos e o gráfico de cosseno em graus? Bem, há uma diferença de escala, pois cos completa um período completo em \(2\pi\) quando medido em radianos, e completa um período completo em 360 ^o quando medido em graus. Mas em termos de forma, não há diferença essencial.

Como usar esta calculadora de gráfico cos?

Esta calculadora de gráfico cos elimina todas as suposições para você, pois tudo o que você precisa fazer é fornecer uma função cos válida. Dependendo do tipo de função cos que você fornecer, você terá um período, ou talvez o período não seja definido, em um caso como \(f(x) = cos(x^2)\), onde ainda dizemos que temos um função cos .

Gráficos cos, junto com gráficos de seno e tangente estão entre os mais comuns. gráficos trigonométricos que você normalmente encontrará.

Exemplo: gráfico de cos

Calcule o gráfico de: \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Solução: A seguinte função foi fornecida:

\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\]

Com base no argumento da função trigonométrica passada, a frequência e o período são calculados da seguinte forma:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

e também

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Portanto, considerando a função trigonométrica fornecida, \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\), obtemos que:

» A amplitude neste caso é \(A = 1/3\).

» A mudança de fase é igual a \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

» O deslocamento vertical é igual a \( 0\).

Resumindo, o seguinte foi encontrado para a função trigonométrica dada

• Período = \(5.0265\)
• Frequência = \(0.1989\)
• Amplitude = \(1/3\)
• Mudança de Fase = \(0.6667\)
• Deslocamento Vertical = \(\displaystyle 0\)

Abaixo está o gráfico correspondente

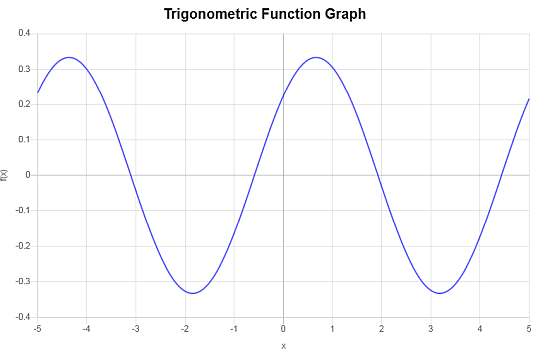
Exemplo: mais gráficos de cos

A seguinte função é periódica? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 - \frac{5}{6}\right)\)

Solução: Não, não é, por causa do termo \(x^2\).

Exemplo: gráfico de cosseno

Calcule o gráfico de: \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Solução: Observe que a expressão trigonométrica passada pode ser simplificada da seguinte forma:

então a função que vamos trabalhar é \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Portanto, com base no argumento da função trigonométrica que foi passada, a frequência e o período são calculados da seguinte forma:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

e também

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Com base na função trigonométrica fornecida, \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\), obtemos que:

» A amplitude neste caso é \(A = 2\).

» A mudança de fase é igual a \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

» O deslocamento vertical é igual a \( 0\).

Resumindo, o seguinte foi encontrado para a função trigonométrica dada

• Período = \(5.0265\)
• Frequência = \(0.1989\)
• Amplitude = \(2\)
• Mudança de Fase = \(0.3667\)
• Deslocamento Vertical = \(\displaystyle 0\)

Abaixo está o gráfico correspondente

Mais calculadoras geométricas

Um dos mais úteis que você pode encontrar é este calculadora de período e frequência , para o qual você fornece qualquer função trigonométrica e receberá a amplitude, o período e a frequência.

Além disso, você pode usar este calculadora de pecado com passos para trabalhar com expressões trigonométricas mais complexas que lidam com a função seno. Seno e cosseno são de fato a pedra angular de tudo o que está relacionado com Geometria e Trigonometria

Além disso, talvez você esteja interessado em avaliando expressões trigonométricas ou gráficos de funções trigonométricas em geral.