Domínio e alcance
O domínio de uma função é um conjunto onde uma função é bem definida. Mais especificamente, seja \(f: D \rightarrow R\) uma função, o que significa que \(f(a)\) está bem definido para \(a \in D\). O domínio da função \(f\) é o conjunto \(D\).
Matematicamente, você escreverá \(dom(f) = D\).
O intervalo de uma função, por outro lado, é um conjunto de valores que podem ser alcançados por meio da função.
Mais especificamente, seja \(f: D \rightarrow R\) uma função, o intervalo é o conjunto de todos os valores possíveis \(b \in R\) para os quais existe \(a \in D\) tal que \(f(a) = b\).
Freqüentemente, o intervalo de uma função é escrito como \(R(f)\) ou também como \(f(D)\) (que também é conhecido como o conjunto de imagens de \(D\) por meio da função \(f\)).
É crucial conhecer o domínio de uma função porque isso nos dá um conjunto seguro de valores nos quais a função está bem definida.
Então, o intervalo é importante porque nos diz quais valores são alcançados pela função. Uma interpretação mais gráfica é esta: Um ponto \(b\) está na faixa de \(f\) se a linha horizontal \(y = b\) cruza o gráfico da função \(f(x)\).
Como calcular o Domínio, em termos práticos?
Aqui está como encontrar domínio e intervalo :
Para o domínio, você precisa primeiro encontrar os pontos onde a função NÃO está definida. As fontes de operações indefinidas são a divisão por zero ou a raiz quadrada de números negativos.
Portanto, você precisa encontrar os pontos (se houver) onde ocorrem essas operações indefinidas. E o domínio será o resto dos pontos, isto é, todos os pontos excluindo aqueles que você encontrar que causam operações indefinidas.
Como calcular o intervalo, em termos práticos?
Seja \(y\) um número e resolveremos para \(x\) a seguinte equação \(f(x) = y\). O valor \(y\) está no intervalo se \(f(x) = y\) puder ser resolvido para \(x\).
Portanto, é um pouco mais complicado: você precisa descobrir se precisa restringir \(y\) de alguma forma para que \(f(x) = y\) tenha uma solução para \(x\).
EXEMPLO 1
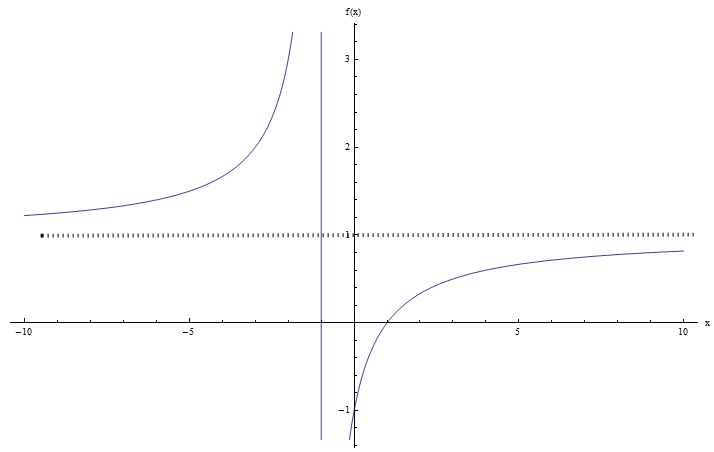
Calcule o domínio e o intervalo da função \(\displaystyle f(x) = \frac{x+1}{x-1}\).
RESPONDA:
Primeiro, calculamos o domínio. Precisamos ver onde a função está bem definida. Normalmente é mais fácil começar onde NÃO está bem definido.
Portanto, neste caso, todas parecem ser operacionais válidas, exceto por uma coisa: o denominador não pode ser zero.
Nota: A chave principal para encontrar o domínio é identificar os pontos onde há divisões potenciais por zero, ou raízes quadradas potenciais de valores negativos, que são operações.
Portanto, uma função é bem definida EXCETO quando \(x-1 = 0\), que ocorre quando \(x = 1\). Portanto, dizemos que o domínio é toda a linha real, exceto pelo valor \(1\).
Usando a notação de intervalo, escreveríamos \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).
Agora precisamos calcular o intervalo. Normalmente, pode ser um pouco mais trabalhoso obter o intervalo do que o domínio, mas vamos lá.
Existem muitas maneiras de encontrar o intervalo: podem confiar na representação gráfica da função para fazer uma afirmação sobre o intervalo de uma função. Isso poderia funcionar, mas não é uma resposta real, apenas um palpite educado.
A outra maneira é a forma matemática formal: Seja \(y\) um número e resolveremos para \(x\) a seguinte equação \(f(x) = y\). O valor \(y\) está no intervalo se \(f(x) = y\) pode ser resolvido para \(x\).
Neste caso, temos:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-1} = y\] \[\Rightarrow \,\,\,x+1=y\left( x-1 \right)\] \[\Rightarrow \,\,\,x+1=yx-y\] \[\Rightarrow \,\,\,x-yx=-1-y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-y\] \[\Rightarrow \,\,\,x=\frac{y+1}{y-1}\]Então, quando \(x\) está bem definido? Quase para todos \(y\), exceto quando \(y = 1\), pois nesse caso temos uma divisão por \(0\). Portanto, o intervalo de \(f\) neste caso é toda a linha real, exceto para 1.
Usando a notação de intervalo, escreveríamos \(R(f) = (-\infty, 1) \cup (1, +\infty)\).
EXEMPLO 2
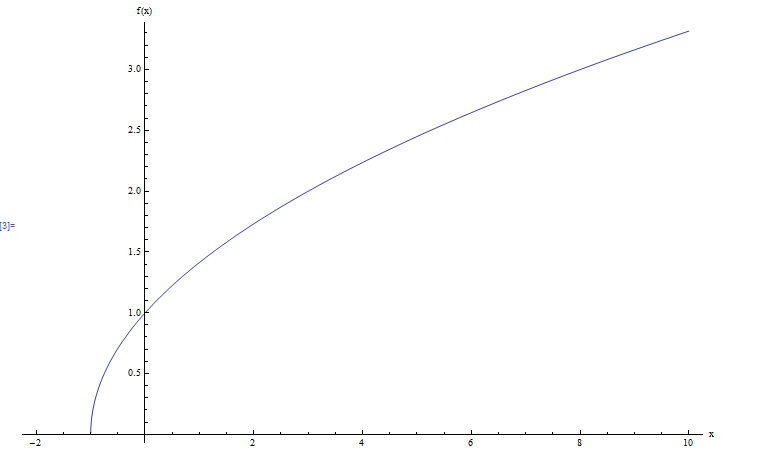
Calcule o domínio e o intervalo da função \(\displaystyle f(x) = \sqrt{x+1}\).
RESPONDA:
Lembre-se, para encontrar o domínio, procurar pontos onde processar ocorrer provavelmente (divisões por zero ou raízes quadradas de valores negativos. Não há divisões neste caso, mas preciso garantir que \(x+1\ge 0\) para que não haja raízes quadradas de valores negativos., Necessário de \(x \ge -1\). Usando a notação de intervalo, escreveríamos \(dom(f) = [-1, +\infty)\).
.Agora, para o intervalo, precisamos resolver para \(x\): \(\sqrt{x+1} = y\). A raiz quadrada de algo nunca é negativa, então pelo menos precisamos desse \(y \ge 0\).
Além disso, ao aplicar o quadrado a ambos os lados, obtemos \(x+1 = y^2\), então a solução é \(x = y^2-1\). Portanto, uma única restrição que requer um \(y\) é que \(y \ge 0\). Portanto, usando uma notação de intervalo, escreveríamos \(R(f) = [0, +\infty)\). Graficamente:
Mais sobre o domínio e intervalo
Um título de resumo, vamos recapitular algumas coisas. Primeiro, o domínio é onde uma função é bem definida, e o intervalo é o conjunto de pontos que são alcançados por meio da função.
Em termos de cálculos de referência, normalmente é mais fácil encontrar o domínio do que o intervalo. Normalmente, algumas pessoas tentam encontrar o intervalo graficamente, mas essa é uma maneira potencialmente menos precisa. As respostas gráficas devem ser interpretadas com cautela.
Você pode conferir tutoriais especificamente sobre como encontrar o domínio e o alcance , que se concentram especificamente em cada caso com mais detalhes.
