Test della linea orizzontale

Questa calcolatrice consente di eseguire il test della retta orizzontale per qualsiasi funzione fornita, mostrando i passaggi. La funzione fornita potrebbe essere qualcosa come "y = 2x - 1", che è il tipo di funzione più semplice funzione lineare oppure si può fornire una funzione più complessa come "y = (2x-1)/(x+1)" che comporta una funzione razionale .

Una volta fornita una funzione valida, è possibile fare clic sul pulsante "Calcola" e verranno fornite tutte le fasi del processo, indicando se la funzione supera o meno il test della linea orizzontale (HLT).

Il funzionamento di questa calcolatrice consiste nell'impostare una linea orizzontale generica e nel verificare quante volte (se mai) la linea attraversa questa linea orizzontale arbitraria. Questo comporta Risolvendo per x l'equazione y = f(x).

Che cos'è il test della linea orizzontale?

L'HLT è un test che permette di valutare se una funzione è o meno uno a uno. Consiste nel tracciare linee orizzontali a diverse altezze e vedere dove si incrociano con il grafico della funzione f(x) data, se lo fanno.

Se nessuna linea orizzontale che si possa immaginare attraversa il grafico della funzione f(x) più di una volta, allora la funzione è uno-a-uno . D'altra parte, se si riesce a trovare una retta orizzontale che attraversa il grafico della funzione f(x) PIÙ DI UNA VOLTA, allora si è dimostrato che la funzione NON è univoca

Quindi potreste pensare: "Aspettate un attimo", questo strumento non serve a dimostrare che una funzione è unidirezionale utilizzando il test della linea orizzontale, ma piuttosto a dimostrare che NON è unidirezionale.

Perché, in pratica, non posso tracciare il grafico di TUTTE le linee orizzontali esistenti per verificare quante volte attraversano il grafico di f(x), ma se trovo UNA linea orizzontale che attraversa il grafico di f(x) troppe volte, allora so che non è uno-a-uno. Quindi, buona riflessione, hai trovato qualcosa di buono.

Utilizzo del test della linea orizzontale nella pratica

Ad esempio, se si dispone della funzione \(f(x) = x^2\), il grafico avrà un aspetto più o meno simile:

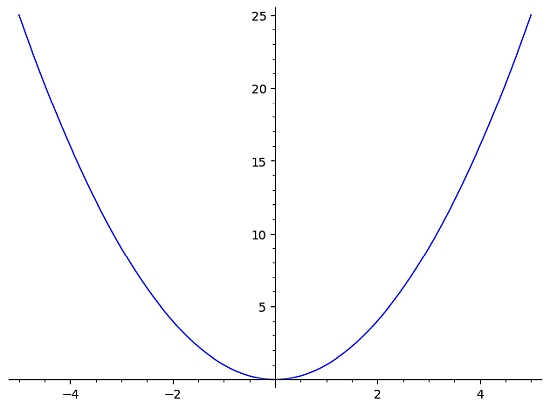
In questo caso, vediamo subito che la funzione non supera il test della retta orizzontale. Perché la retta orizzontale y = 10 mostrata nel grafico sottostante attraversa il grafico di f(x) due volte (più di una)

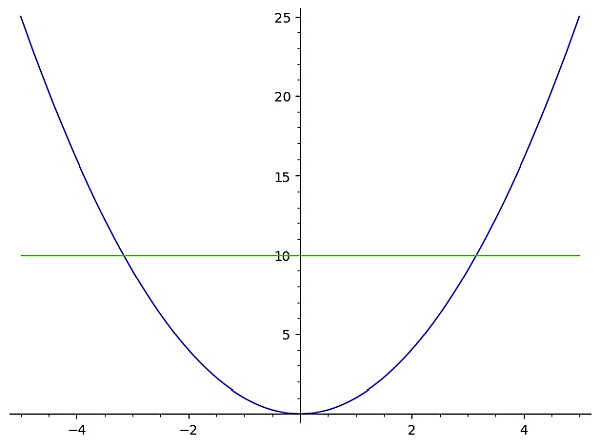
In questo caso, la funzione \(f(x) = x^2\) non supera il test della linea orizzontale e, quindi, non è una funzione funzione uno-a-uno .

Ora, poiché è impossibile testare TUTTE le possibili linee orizzontali, l'HLT deve tentare di utilizzare mezzi algebrici, a meno che non si veda visivamente un chiaro caso di linea orizzontale che farà fallire il test della funzione.

Utilizzo del test della linea orizzontale (analiticamente)

• Passo 1: Partendo da una funzione valida f(x), si imposterà il livello di una linea orizzontale a un valore arbitrario di y
• Passo 2: Quindi si imposta l'equazione: y = f(x), e l'obiettivo è risolvere per x
• Passaggio 3: Non esiste una sola strategia per risolvere questa equazione poiché dipende dalla natura della funzione f(x). Se f(x) è una semplice funzione lineare o quadratica, allora è abbastanza facile risolvere per x. In caso contrario, è necessario provare diversi metodi
• Passaggio 4: Se quando si risolve per x si trova più di una soluzione per una y arbitraria, la funzione non supera l'HLT. Altrimenti, se c'è una sola soluzione o nessuna soluzione, lo supera.

La sottrazione delle frazioni è semplicemente derivata dalla somma delle frazioni: Per sottrarre due frazioni, basta moltiplicare la seconda per -1 e aggiungerla alla prima .

La linea orizzontale può assumere valori negativi o positivi?

La chiave principale dell'implementazione analitica dell'HLT è la scelta di una linea orizzontale arbitraria. Può essere un valore arbitrario, positivo o negativo. Quindi, il valore arbitrario di y utilizzato PUÒ determinare se le soluzioni proposte sono ben definite o meno, ma non aggiunge altre soluzioni, può invece potenzialmente sottrarne.

Ad esempio, se si parte da \(f(x)= \frac{2x+1}{x-1}\) e si risolve x in questo modo: \(y = \frac{2x+1}{x-1}\), si arriva a

\(x = \frac{y+1}{y-2}\)

il che significa che per una data \(y\) si ha ALMENO una soluzione. Perché al massimo una soluzione? Perché quando y = 2 non c'è nessuna soluzione, mentre per qualsiasi altra y c'è una soluzione. Questo funziona benissimo per dimostrare che la funzione supera il test della retta orizzontale.

Esempio: superamento dell'hlt

La seguente funzione supera l'HLT: \(f(x) = \frac{1}{3} x + \frac{5}{4}\) ?

Soluzione:

La funzione fornita è:

\[f\left(x\right) = \frac13x+\frac54\]

Quindi, per valutare se la funzione data supera o meno il test della retta orizzontale, dobbiamo risolvere \(x\) e determinare se non c'è soluzione, se c'è una soluzione o se ci sono più soluzioni. L'equazione di partenza è

\[y=\frac{1}{3}x+\frac{5}{4}\]

Risolvere l'equazione lineare

Mettendo \(x\) sul lato sinistro e \(y\) e la costante sul lato destro otteniamo

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(-\frac{1}{3}\), si ottiene quanto segue

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

e semplificando si ottiene la seguente formula

\[\displaystyle x=3y-\frac{15}{4}\]

Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x = 3y-\frac{15}{4}\).

Poiché risolvendo per \(x\) troviamo una soluzione e si tratta di un'unica soluzione, la funzione data supera il test della retta orizzontale.

Risultati del test della linea orizzontale

Sulla base del lavoro mostrato sopra, si può concludere che la funzione data supera il test della linea orizzontale.

Graficamente, la situazione è rappresentata come segue:

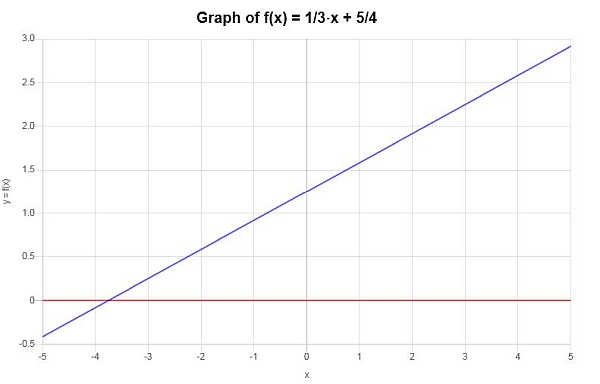
Esempio: questa funzione è one-to-one?

Utilizzando il test della linea orizzontale, indicare se la seguente funzione è uno-a-uno: \(f(x) = x^3 - 1\)

Soluzione: Per valutare se la funzione data supera o meno il test della retta orizzontale, dobbiamo risolvere l'equazione \(y = x^3 - 1\) per \(x\) e determinare se non c'è soluzione, una soluzione o più soluzioni.

Passaggio Iniziale: In questo caso, dobbiamo prima semplificare l'equazione data e per farlo eseguiamo i seguenti passaggi di semplificazione:

Si ottengono quindi le soluzioni:

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

Di queste soluzioni, abbiamo una sola soluzione reale, che è \(x_1=\left(y+1\right)^{\frac{1}{3}}\) . Pertanto, poiché risolvendo \(x\) troviamo una soluzione e si tratta di una sola soluzione reale, la funzione data supera la prova della retta orizzontale.