Calcolatrice di funzioni inverse
Istruzioni: Utilizzate questa calcolatrice per trovare la funzione inversa di una funzione da voi fornita, mostrando tutti i passaggi. Digitare l'espressione della funzione di cui si desidera trovare l'inversa nella casella sottostante.
Ulteriori informazioni su questa calcolatrice di funzioni inverse
Questa calcolatrice consente di trovare l'inversa di una determinata funzione mostrando tutti i passaggi, supponendo che l'inversa esista. La calcolatrice esamina la funzione risolvere un'equazione associato alla definizione della funzione e cercherà di valutare se esiste o meno un'inversa.
Ad esempio, si può fornire una funzione lineare come "f(x) = 3x - 2", che sarebbe un caso semplice, oppure si potrebbe fare un passo avanti con qualcosa di più difficile, come una funzione razionale come "y = (x-1)/(x-3)".
Una volta fornita una funzione valida, fare clic sul pulsante "Calcola" per visualizzare tutte le fasi del processo, con la funzione inversa come risposta finale, se esiste un'inversa, o con la spiegazione che non è stato possibile trovare una soluzione e perché.
Non è garantito che si trovino tutte le funzioni inverse. In primo luogo, non tutte le funzioni hanno un'inversa e in secondo luogo (come vedremo nella prossima sezione), il processo di ricerca dell'inversa comporta Risolvendo per x per un'equazione e, come sappiamo, alcune equazioni possono essere molto difficili o impossibili da risolvere.
Quindi, è più probabile che le funzioni più semplici siano in grado di trovare la loro inversa, nel caso in cui questa esista.

Come si definisce l'inversa di una funzione?
In parole povere, l'inverso di una funzione è la funzione che fa l'opposto di quella originale. Quindi, si può pensare a una funzione in termini di y = f(x), e poi si può pensare di passare da x a y. Si alimenta la funzione con una x, e la funzione dà una y specifica.
La funzione inversa parte dalla y e trova la strada per tornare alla x, in modo che la x sia la stessa che ha portato alla y attraverso la funzione originale. Ora, la definizione formale avviene tramite composizione della funzione . Per una funzione \(f\), si dice che \(g\) è la funzione inversa di \(f\) se
\[ f(g(x)) = x \]E
\[ g(f(x)) = x \]per tutte le x in un certo insieme. C'è dell'altro, ma lo lasceremo a livello intuitivo (a rigor di termini, una funzione deve essere iniettiva e surgiettiva per essere invertibile, e alcuni altri tecnicismi che vengono presi in considerazione, come la limitazione della dominio e raggio d'azione ecc.)
Di solito, chiamiamo \(f^{-1}\) l'inverso di \(f\), quindi la formula che definisce l'inverso è tipicamente scritta come:
\[ f(f^{-1}(x)) = x \]Quali sono i passaggi per trovare la funzione inversa?
- Passo 1: Si inizia con l'equazione che definisce la funzione, cioè si inizia con y = f(x)
- Passo 2: Si utilizza quindi la manipolazione algebrica per risolvere x. A seconda della complessità di f(x), la soluzione di x può essere più facile o più difficile.
- Passaggio 3: In alcune circostanze non sarà possibile risolvere per x, per funzioni complesse non lineari f(x)
- Passaggio 4: Se si è in grado di risolvere per x, allora si dovrebbe essere in grado di scrivere x = g(y)
- Passaggio 5: È necessario valutare se la soluzione trovata è unica. Cioè, è in grado di risolvere x in modo univoco. In altre parole, avete trovato un'unica soluzione quando avete risolto per x? Se sì, allora si ha una funzione inversa, altrimenti non c'è alcuna funzione inversa
- Passaggio 6: Se si è trovata l'inversa risolvendo x = g(y), è sufficiente cambiare il nome della variabile e scrivere f -1 (x) = g(x), il che rende l'accento sul fatto che g(x) È l'inverso effettivo
Se si utilizzasse il calcolo e le derivate (ma si noti che NON è necessario Derivati per calcolare l'inversa), si può trovare la derivata della funzione e assicurarsi che la derivata sia sempre positiva o negativa, per garantire che la funzione sia iniettiva e quindi invertibile.
Ma di solito, la metodologia di Risolvendo per x è molto più appetibile per gli studenti di Algebra di base.
La regola per trovare le funzioni inverse
In realtà non esistono altre regole per calcolare la funzione inversa, se non quella di iniziare con y = f(x) e poi risolvere per x. Una regola del genere sembra piuttosto ampia, perché lo è. Più che una regola, è una metodologia generica per iniziare il processo.
In definitiva, il calcolo dell'inversa dipenderà dalla capacità di risolvere un'equazione e di assicurarsi che la soluzione sia unica. È utile valutare prima il grafico della funzione, in modo da non cercare un'inversa quando è evidente che non esiste.
Cosa guardare in un grafico? Per essere invertibile, una funzione deve essere monotona (crescente o decrescente) su un certo sottodominio. Detto questo, potremmo restringere il dominio di una funzione a un sottodominio più piccolo per trovare l'inversa in un insieme più piccolo, il che è sempre una possibilità.

Come facciamo a sapere con certezza che la funzione ha un'inversa?
Formalmente, l'unico modo per assicurarsi che una funzione abbia un'inversa è assicurarsi che la funzione sia iniettiva (1 a 1). Questo si ottiene calcolando la sua derivata (se esiste) e assicurandosi che sia positiva e negativa ovunque, oppure assicurandosi manualmente che quando si inizia con y = f(x) e si risolve per x, si ottenga sempre una soluzione unica.
Questo può essere visto anche graficamente, utilizzando il test della linea orizzontale: Si traccia una linea orizzontale arbitraria e la funzione f(x) supera il test della linea orizzontale se qualsiasi linea orizzontale tracciata attraversa il grafico della funzione al massimo una volta.

Esempio: trovare la funzione inversa
Trovare l'inversa della seguente funzione: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Soluzione:
Abbiamo la seguente funzione:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Quindi, per trovare l'inversa della funzione data, dobbiamo risolvere \(x\) e determinare se esiste una soluzione o meno. L'equazione di partenza è:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Passaggio 0: In questo caso, dobbiamo prima semplificare l'equazione lineare data e per farlo eseguiamo i seguenti passaggi di semplificazione:
Risolvere l'equazione lineare
Mettendo \(x\) sul lato sinistro e \(y\) e la costante sul lato destro otteniamo
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(-\frac{1}{3}\), si ottiene quanto segue
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]e semplificando si ottiene la seguente formula
\[\displaystyle x=3y-\frac{15}{4}\]Pertanto, la soluzione di \(y\) per l'equazione lineare data porta a \(x=3y-\frac{15}{4}\).
Pertanto, poiché risolvendo per \(x\) troviamo una soluzione e si tratta di una sola soluzione, abbiamo trovato l'inverso.
La funzione inversa
Sulla base del lavoro illustrato sopra, si può concludere che la funzione inversa è:
\[f^{-1}(x) = 3x-\frac{15}{4}\]La funzione inversa può essere rappresentata graficamente come segue:
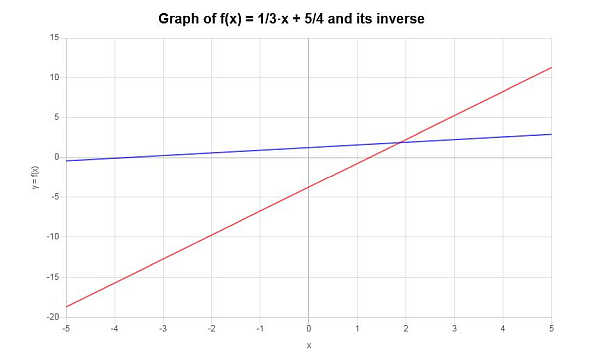
Esempio: altri esempi inversi
Calcolare la funzione inversa di: \(y = \frac{x-1}{x+3}\)
Soluzione:
Per trovare l'inversa della funzione data, risolviamo \(x\) e determiniamo se esiste una soluzione o meno. L'equazione di partenza è:
\[y=\frac{x-1}{x+3}\]Si ottiene quanto segue:
Equazione ausiliaria del numeratore
Dobbiamo porre il numeratore uguale a zero e trovare le soluzioni. Quindi, le radici che non rendono il denominatore uguale a zero saranno le soluzioni dell'equazione razionale
Utilizzando la manipolazione algebrica dell'equazione polinomiale di cui sopra, si ottiene quanto segue:
\[x = -\frac{3y+1}{y-1} \]Equazione ausiliaria del denominatore
Troviamo le radici del denominatore: \(x+3=0\)
Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x=-3\).
Mettere insieme le soluzioni delle equazioni razionali
Poi, controllando che non ci sia uno zero al denominatore, troviamo che la seguente serie di soluzioni all'equazione \(\displaystyle y=\frac{x-1}{x+3}\) è
\[x = -\frac{3y+1}{y-1} \]Poiché quando risolviamo \(x\) troviamo una e una sola soluzione, concludiamo che abbiamo una funzione inversa.
Trovare la funzione inversa
Sulla base del lavoro illustrato sopra, si può concludere che la funzione inversa è:
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]La funzione inversa trovata può essere rappresentata graficamente come segue:
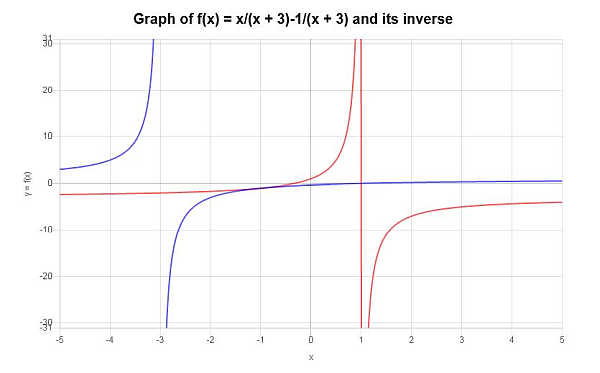
Esempio: non tutte le funzioni hanno un'inversa
La seguente funzione ha un'inversa: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Soluzione: Osservare che
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]che indica che ci sono due soluzioni e che, quindi, in questo caso non esiste un'inversa.
Altre calcolatrici di funzioni
Le funzioni sono un oggetto cruciale in matematica, soprattutto nel calcolo e nell'algebra, dove molte associazioni tra variabili vengono stabilite tramite funzioni.
Ci sono molte cose che si possono fare con la funzione: si può semplificarli , puoi differenziare una funzione è possibile operare su di essi, trovare il composto con un'altra funzione e l'elenco continua.
Molte volte, anche se si parla esplicitamente di funzioni, ci sono funzioni alla base dell'intero processo. Quindi sono presenti, anche se a volte non lo si sa. Una cosa fantastica è che, anche nel caso di funzioni molto complicate, si può sempre rappresentare graficamente una funzione per avere un'idea del suo comportamento, in modo da avere almeno un'idea di cosa fa la funzione (sale, scende, ecc.).




