Funzioni one-to-one
Istruzioni: Utilizzate questa calcolatrice per verificare la presenza di una funzione uno-a-uno, mostrando tutti i passaggi. Digitare la funzione che si desidera verificare nella casella sottostante.
Funzioni one-to-one
Questa calcolatrice vi permetterà di valutare se una funzione è o meno uno-a-uno, mostrandovi tutti i passaggi. La prima cosa da fare è fornire la funzione. Potrebbe trattarsi di qualcosa di semplice, lineare o quadratico, come "y = x^2 - 1", oppure si potrebbe decidere di optare per una funzione funzione razionale come "f(x) = (x-1)/(x+3)".
Quindi, se siete soddisfatti di ciò che avete fornito e vi siete assicurati che la funzione sia valida, fate clic sul pulsante "Calcola", in modo che vi vengano mostrate tutte le fasi del processo.
Il concetto di funzione uno-a-uno è molto importante in Algebra e in Calcolo. Esistono molti modi semplici per verificare l'unicità della funzione, uno di questi è il metodo Test della linea orizzontale ma, data la sua natura, è più facile da usare per confutare che una funzione è uno-a-uno. Per dimostrare che una funzione è unidirezionale, abbiamo bisogno di una funzione equazione risolutiva processo analitico.

Cos'è un processo one-to-one
In parole povere, una funzione univoca o iniettiva è una funzione che per due diversi \(x_1\) e \(x_2\), i valori delle loro immagini attraverso \(f(x)\) sono diversi, il che significa matematicamente
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]Alcuni insegnanti preferiscono scriverla in modo leggermente diverso, ma comunque equivalente: La funzione è uno-a-uno se
\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]Ciò significa, in modo piuttosto sofisticato, che se il grafico della funzione attraversa lo stesso valore (una linea orizzontale), ciò accade solo quando il punto è lo stesso. Quindi, tutto ciò che state dicendo è che non esistono due punti diversi in cui una linea orizzontale la attraversa. Quindi, non fate altro che ribadire il concetto di Test della linea orizzontale .
Come verificare se una funzione è o meno uno-a-uno
- Passo 1: Si parte dalla funzione originale f(x) e si imposta l'equazione y = f(x)
- Passo 2: Tentativo di risolvere per x
- Passaggio 3: Se si trova più di una soluzione, allora la funzione NON è unidirezionale, mentre se ha una sola soluzione o nessuna soluzione, allora la funzione è unidirezionale
Di solito si esegue un'ispezione di base per assicurarsi che la funzione non sia chiaramente uno-a-uno, perché si può facilmente trovare una linea orizzontale per far fallire l'HLT.
In seguito, si cercheranno alcune proprietà visive di base: La funzione è sempre crescente (allora è uno-a-uno), e lo stesso vale per il caso in cui la funzione è sempre decrescente.
Che rapporto c'è tra l'uno e l'altro e la ricerca dell'inverso?
In parole povere, per trovare l'inversa di una funzione, questa DEVE essere uno a uno, almeno in un certo sottodominio. Spesso si restringe il dominio, in modo da rendere una funzione 1 a 1 in un dominio ristretto, che altrimenti non sarebbe 1 a 1.
Ad esempio, \(f(x) = x^2\) non è complessivamente uno a uno. Perché è possibile prendere due punti diversi \(x_1 = -1\) e \(x_2 = 1\) e trovare che \(f(x_1) = (-1)^2 = 1\) e \(f(1) = 1^2 = 1\), il che significa che la proprietà (la caratterizzazione uno-a-uno)
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]non è soddisfatta. Ora, se invece di considerare l'intera linea reale \(\R\), consideriamo solo i valori positivi, possiamo concludere che la funzione è uno-a-uno sui valori reali positivi (Suggerimento: su quel sottodominio, la funzione è crescente)

Esiste una formula per valutare se una funzione è uno-a-uno?
Purtroppo no. Si potrebbe pensare a \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \), come formula uno-a-uno, ma questa è piuttosto una condizione logica che una formula.
Tuttavia, esiste una procedura molto ampia e generica che viene utilizzata per verificare se una funzione è uno-a-uno o meno, che è quella spiegata sopra. Non esiste una "formula uno-a-uno". Se dovessimo sceglierne una, dovrebbe essere y = f(x).
E si risolve per x. Nulla di più, nulla di meno. In definitiva, dipende dal significato di f(x). Una funzione molto complessa e contorta può presentare molte difficoltà per essere risolta, e forse è necessaria una calcolatrice di funzioni, e anche con una calcolatrice di funzioni si può fallire.
Probabilmente starete pensando: perché? Perché, in fondo, non disponiamo di tecniche per risolvere tutte le equazioni. Facciamo solo quello che possiamo con alcuni tipi specifici di equazioni, ma siamo ben lontani dal conoscere un modo ESATTO di risolvere tutte le equazioni.

Esempio: funzione one-to-one
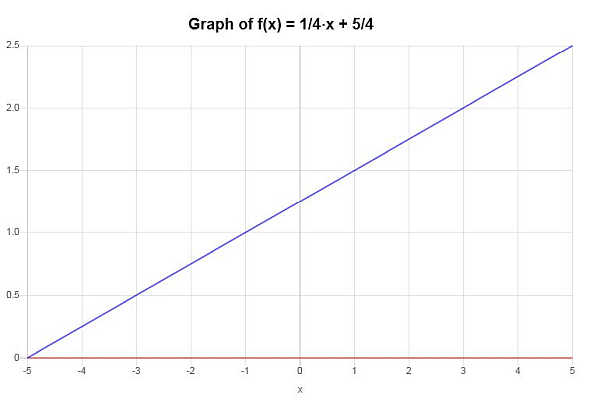
La seguente funzione è iniettiva? \(f(x) = \frac{1}{4} x + \frac{5}{4}\)
Soluzione:
Ci è stata fornita la seguente funzione:
\[f(x) = \frac{1}{4} x + \frac{5}{4}\]Quindi, per valutare se la funzione data è o meno uno-a-uno, dobbiamo risolvere \(x\) e determinare se non c'è soluzione, se c'è una soluzione o se ci sono più soluzioni. L'equazione di partenza è
\[y=\frac{1}{4}x+\frac{5}{4}\]Mettendo \(x\) sul lato sinistro e \(y\) e la costante sul lato destro otteniamo
\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(-\frac{1}{4}\), si ottiene quanto segue
\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]e semplificando si ottiene la seguente formula
\[\displaystyle x=4y-5\]Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x=4y-5\) ed è un'unica soluzione reale, quindi la funzione data è uno-a-uno.
Conclusione
Sulla base di quanto rilevato nella sezione precedente, si può concludere che la funzione data è uno-a-uno.
Graficamente:
Esempio: funzione 1 a 1
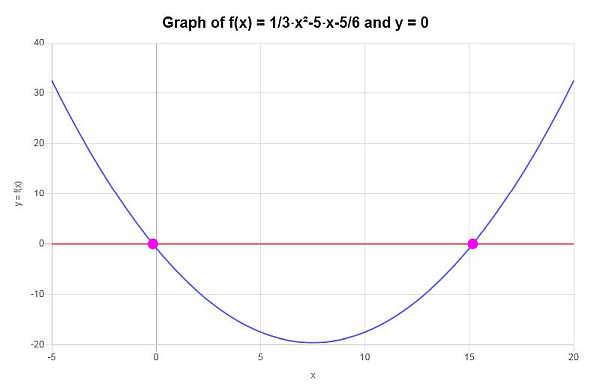
Dimostrare o confutare che la seguente funzione è uno-a-uno: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)
Soluzione: Per valutare se la funzione data è o meno uno a uno, dobbiamo risolvere \(x\) e determinare se non c'è soluzione, se c'è una soluzione o se ci sono più soluzioni. L'equazione di partenza da utilizzare è:
\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]Passaggio Iniziale: In questo caso, dobbiamo prima semplificare l'equazione data e per farlo eseguiamo i seguenti passaggi di semplificazione:
Le soluzioni sono quindi:
\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]Stato di uno a uno
Sulla base del lavoro mostrato sopra, si può concludere che la funzione data NON È UNICA, poiché non supera il test delle linee orizzontali, in quanto ad esempio la linea \(y = 0\) è una linea orizzontale che attraversa la funzione data più di una volta.
Graficamente, la situazione è rappresentata come segue:
Altre interessanti calcolatrici di algebra
Il concetto di funzione 1 a 1 viene solitamente dato per scontato, ma è molto importante, direi critico. Questo perché il concetto di uno-a-uno è strettamente legato all'idea di funzione monotona (funzioni crescenti o decrescenti), così come è strettamente legato al concetto di funzione monotona calcolo della funzione inversa e il suo grafico.
Tuttavia, spesso è difficile distinguere la foresta dagli alberi, poiché la maggior parte dei concetti cruciali dell'Algebra e del Calcolo sono strettamente collegati tra loro. Analisi delle funzioni è una delle cose che si fanno di continuo, quindi è bene acquisire le competenze necessarie per diventare bravi.






