Ulteriori informazioni sul grafico delle funzioni inverse

Questa calcolatrice aiuta a trovare il grafico della funzione inversa fornita, a condizione che la funzione abbia un'inversa, il che non è sempre vero.

È possibile fornire una funzione nel formato "y = 2x - 1", o semplicemente fornire un'espressione come "f(x) = (x-1)/(x-3)" o semplicemente "(x-1)/(x-3)" per specificare la funzione.

Dopo aver fornito una funzione valida, è possibile fare clic sul pulsante "Calcola" e verranno visualizzati tutti i passaggi della procedura calcolo della funzione inversa e se l'inversa esiste, verrà mostrato un grafico con la funzione e l'inversa.

Osserviamo che, affinché la funzione data abbia una funzione inversa, è necessario che la funzione sia uno-a-uno, il che significa che ogni valore nell'intervallo della funzione ha al massimo una preimmagine nel dominio della funzione ed esattamente una preimmagine nell'intervallo effettivo ristretto.

Come sapere se una funzione è invertibile

Prima di ottenere il grafico dell'inversa di una data funzione, è necessario sapere se la funzione ha un'inversa. Il criterio principale per avere un'inversa è l'essere uno-a-uno, il che significa che un valore nell'intervallo non può avere due valori associati (preimmagini).

Forse gli studenti preferiscono non usare termini tecnici come "immagini" e "preimmagini", e anche se si tratta di concetti fondamentali della teoria delle funzioni, in questo caso possiamo usare un semplice test grafico per valutare se una funzione è o meno uno-a-uno, e quindi se è possibile trovare e tracciare il grafico della sua inversa.

Test della linea orizzontale

Il test della retta orizzontale indica che, affinché una funzione sia unidirezionale, qualsiasi retta orizzontale costruita deve attraversare il grafico della funzione al massimo una volta. Se si riesce a trovare una linea orizzontale che attraversa il grafico della funzione data più di una volta, allora la funzione NON è unidirezionale.

Ad esempio, la funzione mostrata di seguito è una funzione uno-a-uno, perché qualunque sia la linea orizzontale che le viene lanciata, essa attraverserà il grafico della funzione esattamente una volta:

Ma l'esempio successivo mostra una funzione che non è uno-a-uno, perché vediamo una linea orizzontale che attraversa la linea della funzione 2 volte (più di una volta):

Passi per trovare il grafico inverso

• Passo 1: Esistono due metodi comuni: uno è il metodo grafico e l'altro è il metodo analitico
• Passo 2: Per il metodo grafico, è necessario prima applicare il test della linea orizzontale e assicurarsi che lo superi, in modo che sia uno-a-uno, e l'inverso esiste
• Passaggio 3: Poi, si traccia la retta y = x nel grafico (una retta che ha un angolo di 45 ^o gradi rispetto all'asse x
• Passaggio 4: Dopodiché si usa semplicemente la retta y = x come "specchio" e si riflettono i punti del grafico originale rispetto allo "specchio". Il grafico ottenuto con questo processo di specchiatura è il grafico dell'inversa
• Passaggio 5: Per il metodo analitico, è necessario prima algebricamente trovare l'inverso : Si inizia con y = f(x) e poi si risolve per y.
• Passaggio 6: Se esiste un'unica soluzione, allora esiste l'inversa e si scrive x = g(y). Adattando i nomi delle variabili, si definisce formalmente la funzione inversa \(f^{-1}\) in termini di g
• Passaggio 7: Infine, si tracci il grafico dell'inverso trovato \(f^{-1}\) come si farebbe per rappresentare graficamente una funzione normalmente

Quando si deve trovare il grafico di un'inversa, sia il metodo grafico che quello analitico vanno bene, solo che il metodo analitico ha un vantaggio, ovvero quello di calcolare la funzione inversa durante il processo, per cui si finisce per avere un'espressione matematica della stessa, non solo il suo grafico.

Perché tracciare il grafico dell'inverso

Ci sono molti motivi per farlo. In primo luogo, la funzione inversa è di per sé un attore molto importante nella teoria delle funzioni, poiché una funzione mostra come passare da una x a una y, quindi è naturale voler sapere qual è il meccanismo per passare da y a x, ed è proprio questo che la funzione inversa ci fornisce.

Si può quindi pensare a una funzione come a una mappa a senso unico da un punto "X" a un punto "Y", e calcolare la funzione inversa è come definire esplicitamente una mappa per andare da "Y" a "X".

E poi il grafico dell'inversa vi dirà molte informazioni sulla funzione inversa: se scende verso l'alto, come si comporta.

Come mi aiuta questa calcolatrice di funzioni con grafico inverso?

In primo luogo, questa calcolatrice analizza la funzione per vedere se è invertibile utilizzando il metodo analitico e, se è possibile trovare tale inversa, ne traccia il grafico.

Trovare l'inverso comporta risolvere un'equazione che non è un compito facile, a meno che non si abbia a che fare con Equazioni lineari O equazioni polinomiali ma a parte questo, il processo può essere molto complesso o addirittura impossibile.

Altre calcolatrici possono eseguire un processo simile, ma uno dei vantaggi di questa calcolatrice è che fornisce tutte le fasi del processo, con una spiegazione dettagliata, ove possibile.

Esempio: trovare il grafico dell'inversa

Grafico dell'inverso di : \( y = \frac{2}{3} x - \frac{5}{6}\)

Soluzione:

Ci è stata fornita la seguente funzione:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Quindi, per trovare l'inversa della funzione data, dobbiamo risolvere \(x\) e determinare se esiste una soluzione o meno. L'equazione di partenza è

\[y=\frac{2}{3}x-\frac{5}{6}\]

Passaggio 0: In questo caso, dobbiamo prima semplificare l'equazione lineare data e per farlo eseguiamo i seguenti passaggi di semplificazione:

Risolvere l'equazione lineare

Mettendo \(x\) sul lato sinistro e \(y\) e la costante sul lato destro otteniamo

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(-\frac{2}{3}\), si ottiene quanto segue

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

e semplificando si ottiene la seguente formula

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Pertanto, la soluzione di \(y\) per l'equazione lineare data porta a \(x = \frac{3}{2}y+\frac{5}{4}\).

Pertanto, poiché risolvendo per \(x\) troviamo una soluzione e si tratta di una sola soluzione, abbiamo trovato l'inverso.

La funzione inversa trovata

Sulla base del lavoro illustrato sopra, si può concludere che la funzione inversa è:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

La funzione inversa può essere rappresentata graficamente come segue:

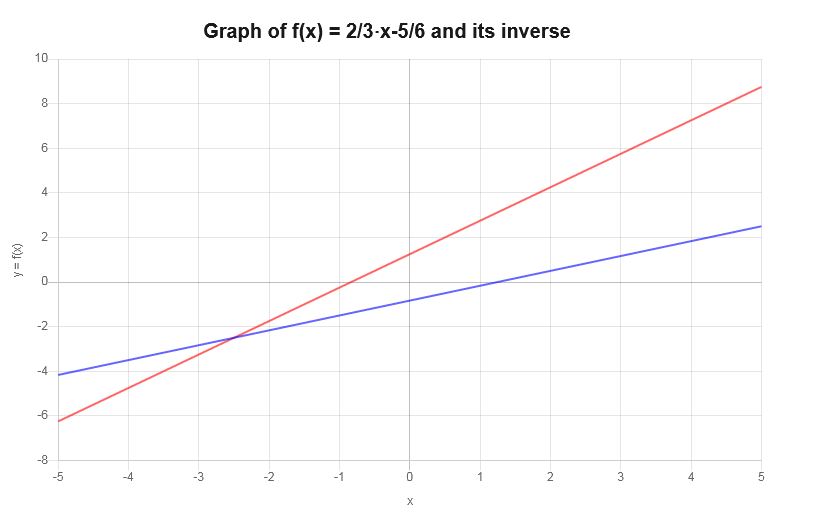
Esempio: altri grafici inversi

È possibile trovare il grafico inverso di: \(y = x^2\)

Soluzione: No, non possiamo trovare il grafico dell'inversa di \(y = x^2\), poiché questa funzione non supera il test della retta orizzontale. Un altro modo di vedere la questione è che risolvendo \(x\) si ottiene \(x = \pm \sqrt y\), e poiché troviamo due soluzioni, non c'è l'inversa e di conseguenza non c'è il grafico dell'inversa.

Altre calcolatrici di funzioni

Le funzioni e qualsiasi tipo di operazione sulle funzioni sono il vero centro dell'Algebra e del Calcolo. Una buona Calcolatrice di funzioni vi semplificherà la vita in termini di riduzione di una funzione alla sua espressione più semplice.

Allora, avrete una buona strumento per la creazione di grafici di funzioni per dare una rapida occhiata alle proprietà grafiche di una funzione. Vedere il grafico di una funzione può dire molto sul suo comportamento, anche prima di guardare la sua espressione algebrica.

Poi ci sono operazioni più avanzate, come la ricerca della derivata, per la quale questo Calcolatrice di differenziazione è utile, in quanto mostra tutte le fasi del processo. Come previsto, la derivata della funzione inversa presenta un'interessante associazione con la derivata della funzione originale.