Dominio e intervallo
Il dominio di una funzione è un insieme in cui una funzione è ben definita. Più specificamente, sia \(f: D \rightarrow R\) una funzione, il che significa che \(f(a)\) è ben definito per \(a \in D\). Il dominio della funzione \(f\) è l'insieme \(D\).
Matematicamente scriverai \(dom(f) = D\).
Il range di una funzione, invece, è un insieme di valori che possono essere raggiunti tramite la funzione.
Più specificamente, sia \(f: D \rightarrow R\) una funzione, l'intervallo è l'insieme di tutti i valori possibili \(b \in R\) per cui esiste \(a \in D\) tale che \(f(a) = b\).
Spesso, l'intervallo di una funzione viene scritto come \(R(f)\) o anche come \(f(D)\) (noto anche come set di immagini di \(D\) tramite la funzione \(f\)).
È fondamentale conoscere il dominio di una funzione perché questo ci fornisce un insieme sicuro di valori su cui la funzione è ben definita.
Quindi, l'intervallo è importante perché ci dice a quali valori vengono raggiunti dalla funzione. Un'interpretazione più grafica è questa: un punto \(b\) è nell'intervallo di \(f\) se la linea orizzontale \(y = b\) interseca il grafico della funzione \(f(x)\).
Come calcolare il dominio, in termini pratici?
Ecco come trovare dominio e intervallo :
Per il dominio, devi prima trovare i punti in cui la funzione NON è definita. Le fonti di operazioni indefinite sono la divisione per zero o la radice quadrata di un numero negativo.
Quindi, è necessario trovare quei punti (se presenti) in cui si verificano quelle operazioni indefinite. E il dominio sarà il resto dei punti, cioè tutti i punti esclusi quelli che trovi che causano operazioni indefinite.
Come calcolare la gamma, in termini pratici?
Sia \(y\) un numero e risolveremo per \(x\) la seguente equazione \(f(x) = y\). Il valore \(y\) è compreso nell'intervallo se \(f(x) = y\) può essere risolto per \(x\).
Quindi questo è un po 'più complicato: devi trovare se hai bisogno di limitare \(y\) in qualche modo in modo che \(f(x) = y\) abbia una soluzione per \(x\).
ESEMPIO 1
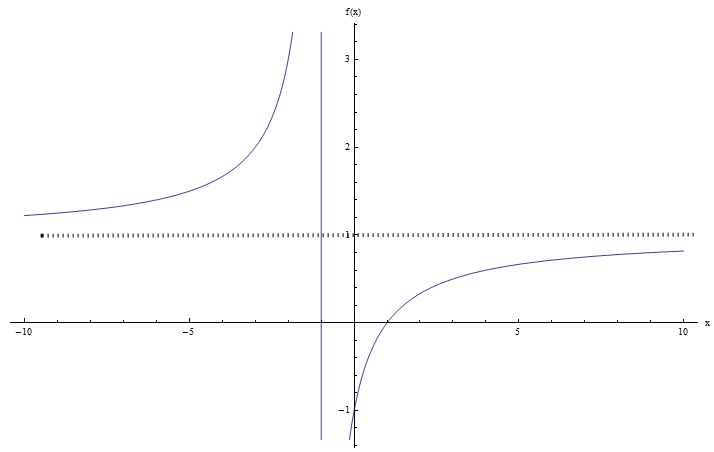
Calcola il dominio e l'intervallo della funzione \(\displaystyle f(x) = \frac{x+1}{x-1}\).
RISPOSTA:
Innanzitutto, dobbiamo calcolare il dominio. Dobbiamo vedere dove la funzione è ben definita. Di solito è più facile iniziare da dove NON è ben definito.
Quindi in questo caso, tutte sembrano essere operazioni valide, tranne una cosa: il denominatore non può essere zero.
Nota: La chiave principale per trovare il dominio è identificare i punti in cui ci sono potenziali divisioni per zero, o potenziali radici quadrate di valori negativi, che sono operazioni non valide.
Quindi, la funzione è ben definita TRANNE quando \(x-1 = 0\), che si verifica quando \(x = 1\). Quindi, diciamo che il dominio è l'intera linea reale eccetto per il valore \(1\).
Usando la notazione dell'intervallo, scriveremmo \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).
Ora dobbiamo calcolare l'intervallo. In genere, potrebbe essere un po 'più laborioso ottenere l'intervallo di quanto non lo sia per ottenere il dominio, ma eccoci qui.
Esistono molti modi per trovare l'intervallo: alcuni possono fare affidamento sulla rappresentazione grafica della funzione per fare un'affermazione sull'intervallo di una funzione. Potrebbe funzionare, ma non è una vera risposta, solo un'intuizione colta.
L'altro modo è il modo matematico formale: Sia \(y\) un numero emo risolvere per \(x\) la seguente equazione \(f(x) = y\). Il valore \(y\) è compreso nell'intervallo se \(f(x) = y\) può essere risolto per \(x\).
In questo caso abbiamo:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-1} = y\] \[\Rightarrow \,\,\,x+1=y\left( x-1 \right)\] \[\Rightarrow \,\,\,x+1=yx-y\] \[\Rightarrow \,\,\,x-yx=-1-y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-y\] \[\Rightarrow \,\,\,x=\frac{y+1}{y-1}\]Quindi, quando \(x\) è ben definito? Quasi per tutti \(y\), tranne quando \(y = 1\), perché in quel caso abbiamo una divisione per \(0\). Quindi, l'intervallo di \(f\) in questo caso è l'intera linea reale, tranne 1.
Usando la notazione dell'intervallo, scriveremmo \(R(f) = (-\infty, 1) \cup (1, +\infty)\).
ESEMPIO 2
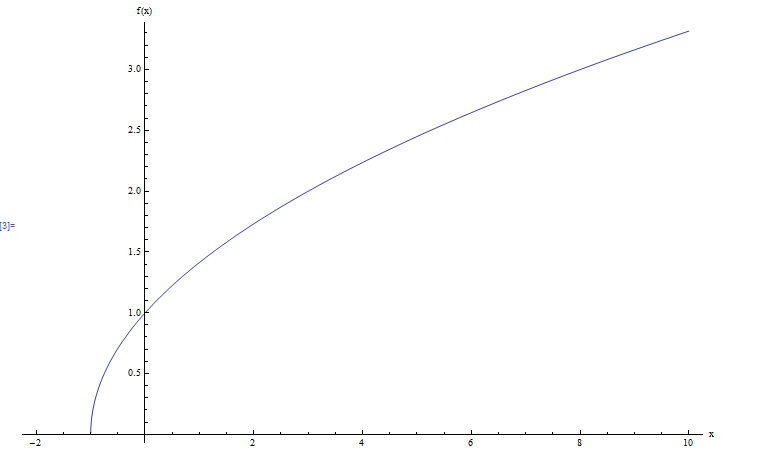
Calcola il dominio e l'intervallo della funzione \(\displaystyle f(x) = \sqrt{x+1}\).
RISPOSTA:
Ricorda, per trovare il dominio dobbiamo cercare i punti in cui possono verificarsi operazioni non valide. Non ci sono divisioni in questo caso, ma dobbiamo assicurarci che \(x+1\ge 0\) in modo che non ci siano valori negativi. Quindi abbiamo bisogno di \(x \ge -1\). Usando la notazione dell'intervallo, scriveremmo \(dom(f) = [-1, +\infty)\).
.Ora per l'intervallo, dobbiamo risolvere per \(x\): \(\sqrt{x+1} = y\). La radice quadrata di qualcosa non è mai negativa, quindi almeno abbiamo bisogno di \(y \ge 0\).
Inoltre, applicando il quadrato su entrambi i lati, otteniamo \(x+1 = y^2\), quindi la soluzione è \(x = y^2-1\). Quindi, l'unica restrizione che dobbiamo imporre a \(y\) è quella \(y \ge 0\). Quindi, usando la notazione dell'intervallo, scriveremmo \(R(f) = [0, +\infty)\). Graficamente:
Ulteriori informazioni sul dominio e sulla portata
Per riassumere, ricapitoliamo alcune cose. Innanzitutto il dominio è dove una funzione è ben definita e l'intervallo è l'insieme di punti che vengono raggiunti attraverso la funzione.
In termini di calcoli richiesti, in genere è più facile trovare il dominio che trovare l'intervallo. Normalmente, alcune persone cercano di trovare graficamente l'intervallo, ma questo è un modo meno preciso. Le risposte grafiche devono essere interpretate con cautela.
Puoi controllare i tutorial specifici su vieni a trovare il dominio e la gamma , che si concentrano su ciascun caso in modo più dettagliato.
