En savoir plus sur le modèle log-log

Cette calculatrice vous permettra de calculer un modèle de régression log-log pour les données que vous fournissez. Ces données doivent refléter de manière appropriée un modèle log-log, dans lequel il doit y avoir un degré d'association linéaire raisonnable entre ln(X) et ln(Y).

Une fois que vous aurez fourni des données valides, ce qui dans ce cas signifie des données positives pour X et Y, vous devrez cliquer sur le bouton « Calculer » pour commencer afin de pouvoir voir toutes les étapes du processus.

Le modèle log-log a de fortes applications pratiques, notamment dans le domaine de l'économie, dans lequel il est utilisé pour calculer les élasticités .

Qu'est-ce que le modèle log-log ?

Le modèle log-log, comme son nom pourrait le suggérer, est un modèle dans lequel \(\ln(X)\) présente un degré significatif d'association linéaire avec \(\ln(Y)\). Sur la base de ce fait, s'il devient approprié de calculer un modèle de régression pour ces données de transformation, nous recherchons donc les coefficients de régression \(a\) et \(b\) pour estimer

\[\displaystyle \ln(Y) = a + b \ln(X)\]

Ainsi, un calculateur d’un modèle log-log se réduit à un calcul d’un modèle de régression régulier pour les données transformées \(\ln(X)\) et \(\ln(Y)\).

Étapes pour estimer un modèle log-log

• Étape 1 : Identifiez clairement les variables données par X et Y. Assurez-vous qu'elles ont la même taille d'échantillon et qu'elles sont TOUTES DEUX positives, sinon vous ne pouvez pas exécuter un modèle log-log
• Étape 2 : Transformez les données originales X et Y en auxiliaires ln(X) et ln(x)
• Étape 3 : Utilisez une équation de modèle de régression régulière, dans laquelle vous calculez la pente et Interception Y pour vos données transformées en logarithme ln(X) et ln(Y)

Une fois que vous avez estimé les coefficients de régression correspondants, vous pouvez écrire l'équation \(\displaystyle \ln(Y) = a + b \ln(X)\), que vous pouvez soit laisser telle quelle, soit la transformer comme suit :

\[\displaystyle Y = e^a \cdot x^b \]

Interprétation du modèle log-log

Comment pouvons-nous interpréter les coefficients trouvés de la même manière que nous l'avons fait avec la régression habituelle du point de vue du changement marginal ? Pour un problème de régression typique, vous avez le coefficient de pente qui peut être interprété comme l'augmentation moyenne de la variable Y lorsque la variable X est augmentée d'une unité.

Dans un modèle log-log, cela ne fonctionne pas tout à fait comme cela, mais cela a une interprétation marginale similaire. En fait, dans un modèle \(\displaystyle \ln(Y) = a + b \ln(X)\), nous pouvons l'interpréter comme suit :

Une augmentation de 1% de X entraîne une augmentation moyenne de Y de b% . Naturellement, si \(b\), cela correspond à une diminution.

Pourquoi nous utilisons ce type de modèle

L'une des raisons les plus importantes est qu'il s'applique largement à l'économie. L'idée selon laquelle l'élasticité-prix de la demande est simplement déterminée en calculant le coefficient de pente d'un modèle log-log est suffisamment pertinente pour qu'on l'étudie.

En outre, l’idée d’un changement marginal relatif a de nombreuses autres applications dans la théorie de l’utilité en économie, ce qui en fait un modèle extrêmement pratique et applicable.

Exemple de calcul de régression log-log

Considérez les données suivantes pour X et Y :

X: 1, 2, 3, 4, 5, 6, 7

Y : 10, 11,1, 13, 15,6, 16,8, 20, 22,4

Estimez le modèle log-log correspondant et présentez un nuage de points approprié

Solution :

qui conclut le calcul.

Plus de calculateurs de régression

Vous devrez évaluer si vous avez un coefficient de corrélation significatif entre ln(X) et ln(Y) avant d'exécuter le modèle. C'est également une bonne idée faire un nuage de points des données pour voir si elles sont cohérentes avec ce qui est attendu d'une association log-log.

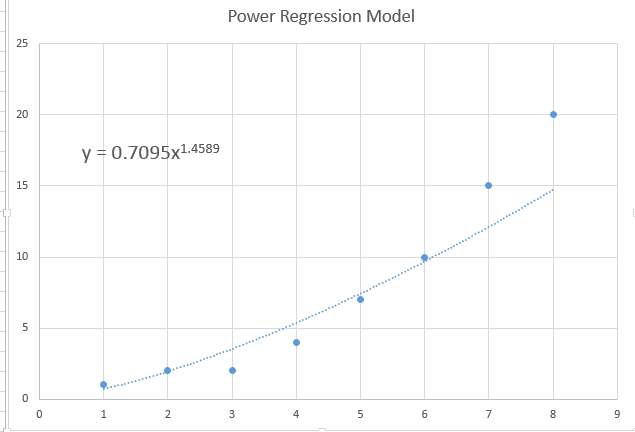
Souvent, il n'y a qu'un niveau subtil de courbure et les données montreront un modèle presque plat, ce qui est également cohérent avec un modèle de régression traditionnel, mais cela peut aussi être un modèle de régression de puissance avec de très petits coefficients..