À propos de ce calculateur de régression exponentielle

Les diagrammes de dispersion sont utilisés pour évaluer le type d'association entre une variable indépendante \(X\) et une variable dépendante \(Y\). En général, une ligne droite, appelée ligne de régression, est également tracée avec un diagramme de dispersion.

De plus, quel que soit le degré d'association linéaire entre les variables, la ligne de régression est généralement ajoutée, quel que soit le degré. Cela peut parfois être trompeur lorsque les données ne suivent pas un modèle linéaire mais plutôt un modèle non linéaire, le modèle exponentiel étant un modèle couramment rencontré.

Comment calculer la régression exponentielle ?

Tout d'abord, vous devez disposer de paires de données de la forme \((X_i, Y_i)\). Normalement, lorsque ces données sont au moins vaguement regroupées autour d'une ligne droite, un modèle de régression linéaire est calculé en calculant ses coefficients via la méthode des moindres carrés.

Parfois, les données ne suivent pas un modèle linéaire et, plus précisément, il existe un modèle de croissance rapide dans la variable dépendante \(Y\) lorsque les valeurs de la variable indépendante \(X\) augmentent.

Lorsque cela se produit, vous utilisez également le Technique des moindres carrés pour calculer les coefficients du modèle exponentiel, seulement qu'au lieu d'appliquer sur les \(X\) et les \(Y\), vous faites une petite astuce et appliquez sur les logarithmes des \(X\) et des \(Y\).

Comment pouvez-vous effectuer une régression exponentielle à la main ?

En fait, ce n'est pas recommandé. La représentation graphique d'un nuage de points , calcul des paramètres du modèle, en utilisant le formule de régression exponentielle et la représentation graphique du modèle exponentiel a nécessité une bonne dose de calculs mathématiques, pour lesquels il est très difficile de le faire à la main. La formule du modèle est

\[ Y = a e^{b x} + \varepsilon \]

Il est fortement recommandé d'utiliser une calculatrice de statistiques en ligne comme celle-ci, ou sinon Excel ou votre calculatrice scientifique préférée, mais l'option « à la main » est pratiquement hors de question.

La régression exponentielle est-elle linéaire ?

Non, ce n'est pas le cas. Le modèle exponentiel commence à croître plus rapidement à mesure que \(X\) augmente, tandis que le modèle linéaire croît au même rythme que \(X\).

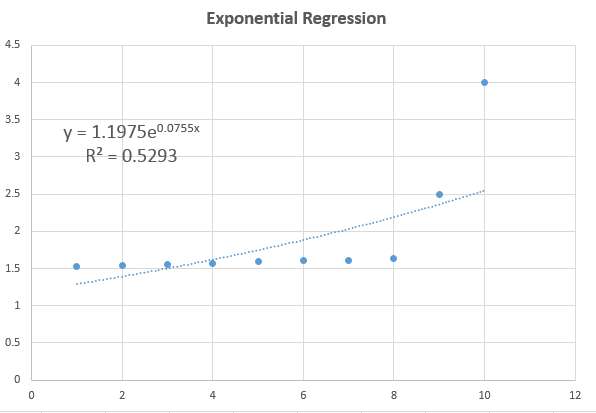
Quelle est la différence entre la régression de puissance et la régression exponentielle ?

Il y a une différence structurelle. En effet, dans un modèle exponentiel, le « X » apparaît comme l'exposant dans le modèle, alors que dans la régression de puissance le « X » apparaît dans la base, ce qui conduit à un taux de croissance beaucoup plus rapide pour des valeurs plus grandes de \(X\) pour le modèle exponentiel.

Quels autres outils graphiques puis-je utiliser ?

Vous pouvez utiliser d'autres outils de création de graphiques dans différentes circonstances. Par exemple, si vous pensez ou savez qu'une régression linéaire est appropriée, vous pouvez utiliser celui-ci Créateur de diagrammes de dispersion avec un Calculateur de régression linéaire .

D'autre part, observez que s'il y a absence d'un modèle linéaire parce que le rythme de croissance ne semble pas être constant lorsque X augmente, cela pourrait être le cas, mais il ne doit pas nécessairement s'agir d'un modèle exponentiel, car il peut également s'agir d'un modèle de régression de puissance ou d'un modèle de régression polynomiale