En savoir plus sur cette calculatrice d'ordonnée à l'origine avec étapes.

L'ordonnée à l'origine d'une ligne est le point où la ligne croise l'axe \(y\), et c'est un point très pertinent dans de nombreux contextes.

Pour utiliser cette calculatrice, vous devez suivre les étapes suivantes :

1. Sélectionnez une façon de définir la ligne. Vous pouvez réellement fournir un équation de la droite , fournissez deux points de la droite, ou un point de la droite et la pente
2. Assurez-vous de choisir au moins une des méthodes et de fournir les informations requises pour l'option sélectionnée
3. Cliquez sur "Calculer"

Comment calculer l'ordonnée à l'origine ?

La façon dont vous calculez l'ordonnée à l'origine dépend de la façon dont vous avez spécifié la ligne. Souvent, vous pouvez regarder le graphique de la ligne et plus ou moins estimer où elle croise l'axe y, qui est le trouver l'ordonnée à l'origine sur la méthode graphique .

De cette façon, vous pouvez alors avoir une idée au moins de la valeur approximative de l'ordonnée à l'origine

Comment trouver l'ordonnée à l'origine avec la pente ?

La manière idéale, cependant, est de calculer algébriquement l'ordonnée à l'origine. Par exemple, lorsque vous avez le équation sous forme d'intersection de pente, en utilisant la formule de la ligne.

\[y = mx + n\]

vous savez déjà que l'ordonnée à l'origine est \(n\). Pourquoi? car \(y\), en fonction de \(x\) est \(y = mx + n\). Ensuite, lorsque x = 0, nous obtenons \(y = n\), et nous savons que \(x = 0\) est le point où le graphique croise l'axe des y

L'ordonnée à l'origine est-elle un nombre ou une paire (x, y) ?

Cela dépend un peu de la convention que vous utilisez. Si la valeur y à laquelle la ligne croise l'axe y est \(y_{intercept}\), alors la manière la plus couramment utilisée est que l'ordonnée à l'origine soit la paire \((0, y_{intercept})\).

Cependant, si vous dites que l'ordonnée à l'origine est juste \(y_{intercept}\), c'est également correct, seulement que certains instructeurs vous demanderont d'écrire l'ordonnée à l'origine comme une paire ordonnée.

Mais la coordonnée x de l'ordonnée à l'origine est TOUJOURS 0, donc certaines personnes trouvent redondant d'écrire la paire complète.

Puis-je obtenir le calculateur d'ordonnée à l'origine à partir de deux points ?

Oui. Dans ce cas, vous devez d'abord utiliser le deux points pour trouver la pente , en utilisant la formule suivante

\[m = \frac{y_2 - y_1}{x_2 - x_1} \]

Une fois que vous avez la pente, vous pouvez construire la forme point-pente en utilisant

\[y - y_1= m (x -x_1)\]

Et puis en résolvant pour \(y\) vous obtiendrez le Forme d'interception de pente , qui vous donne directement l'ordonnée à l'origine

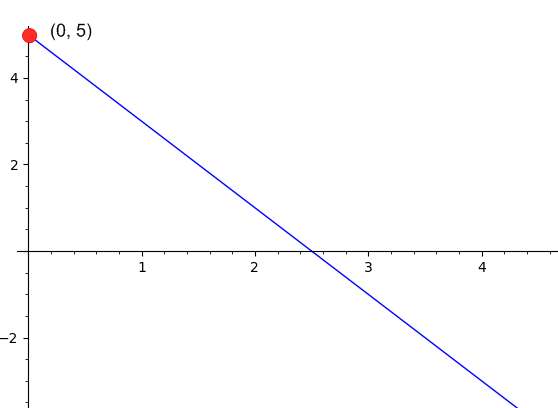
Exemple : calcul de l'ordonnée à l'origine étant donné deux lignes

Vous savez qu'une droite passe par les points \(\left(\displaystyle \frac{1}{4}, 1\right)\) et \(\left(\displaystyle \frac{15}{2}, 6\right)\). Trouvez l'ordonnée à l'origine de la droite.

Solution: : Calcul de l'ordonnée à l'origine de la droite

L'information fournie sur la ligne est que la ligne passe par les points\(\displaystyle \left( \frac{1}{4}, 1\right)\) et \(\displaystyle \left( \frac{15}{2}, 6\right)\)

Par conséquent, la première étape consiste à calculer la pente. La formule de la pente est : \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Maintenant, en branchant les nombres correspondants est , on obtient que la pente est : \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 6 - 1}{ \displaystyle \frac{15}{2} - \frac{1}{4}} = \frac{ \displaystyle 6-1}{ \displaystyle \frac{15}{2}-\frac{1}{4}} = \frac{20}{29}\]

Alors, maintenant nous savons que la pente est \(\displaystyle m = \frac{20}{29}\) et que la droite passe par le point \(\displaystyle \left( \frac{1}{4}, 1\right)\)

Par conséquent, avec les informations dont nous disposons, nous pouvons construire directement la forme point-pente de la ligne, qui est

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

puis en branchant les valeurs connues de \(\displaystyle b = \frac{20}{29}\) et \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{4}, 1\right)\), on obtient que

\[\displaystyle y-1 = \frac{20}{29} \left(x-\frac{1}{4}\right)\]

Maintenant, nous devons développer le côté droit de l'équation en distribuant la pente, nous obtenons donc \[\displaystyle y = \frac{20}{29} x + \frac{20}{29} \left(-\frac{1}{4}\right) + 1\]

et en simplifiant on obtient que \[\displaystyle y=\frac{20}{29}x+\frac{24}{29}\]

Conclusion : Sur la base des données fournies, nous concluons que la ligne croise l'axe des ordonnées à \(\displaystyle y = \frac{24}{29}\), par conséquent, le point d'intersection y correspondant est \(\displaystyle \left(0, \frac{24}{29}\right)\).

Un autre calcul qui pourrait également vous intéresser est celui qui utilise notre calculateur d'abscisse , qui est le point où la ligne croise l'axe des x.

Les interceptions d'une ligne fournissent une excellente intuition graphique de ce que fait la ligne, et elles ont des applications directes lorsque résoudre des systèmes d'équations , ou en économie lors du calcul des surplus des consommateurs et des producteurs.