En savoir plus sur cette calculatrice graphique cos

Cette calculatrice vous permettra de générer le graphique de n'importe quelle fonction cosinus, ainsi que le l'amplitude, la période et la fréquence en montrant toutes les étapes. Vous devez fournir une fonction valide impliquant la fonction cosinus. Il peut s'agir de quelque chose de trivial comme cos(x), ou de quelque chose de plus compliqué comme 2*cos(1/3 x + pi) - 4/5.

Une fois que vous avez fourni une fonction valide impliquant le cosinus, il vous suffit de cliquer sur "Calculer" pour obtenir les résultats et toutes les étapes du processus indiqué.

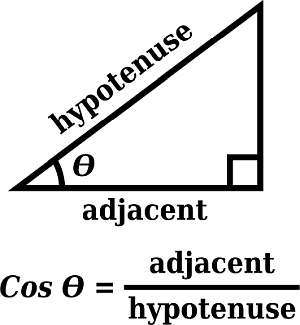
Le cosinus est un fonction trigonométrique qui a une myriade d'applications en mathématiques et en physique. Il est également couramment utilisé en géométrie, lorsque résolution de triangles .

Comment faire un graphique en cos ?

Le principe de base de la représentation graphique de tout type de fonction est de recourir à une fonction simple connue dont on connaît le graphe, puis de construire le graphe que l'on souhaite trouver en se basant sur des translations et des changements d'échelle de ce graphe simple.

Dans le cas du graphique du cosinus, nous savons que l'expression la plus simple d'une fonction cosinus est f(x) = cos(x), dont le graphique est illustré ci-dessous :

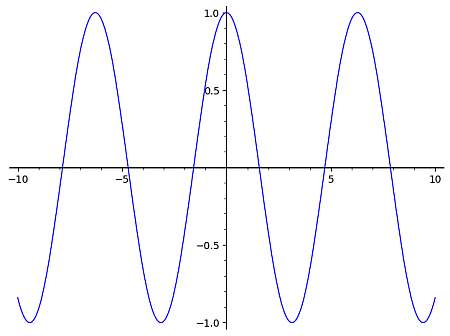
Nous pouvons ensuite utiliser ce graphique de base pour dériver le graphique de fonctions cos plus complexes, car la forme générale sera la même, sauf qu'elle peut potentiellement être déplacée vers la gauche ou la droite, vers le bas ou vers le haut, et que la période peut également changer, selon la fonction fournie.

Quelles sont les étapes de la représentation graphique d'une fonction cosinus ?

• Étape 1 : Identifiez la fonction cos que vous voulez représenter sous la forme a*cos(bx+c)+d si possible
• Étape 2 : La valeur de a correspondra à la amplitude d est l'unité le graphique du cos de base est translaté vers le haut, et le graphique est décalé de -c/b vers la droite
• Étape 3 : Si la fonction cos n'est pas sous la forme a*cos(bx+c)+d, créez un tableau de valeurs pour x et f(x) (où f(x) est la fonction cos donnée), et calculez plusieurs points que vous pouvez utiliser pour tracer manuellement la forme du graphique cos

En effet, seules les fonctions de la forme a*cos(bx+c)+d auront une expression claire pour l'amplitude, la période, la fréquence et les translations, mais ce ne sont pas les seules fonctions cosinus que vous pouvez concevoir. Par exemple, \(f(x) = cos(x^2)\) est une fonction cosinus, mais elle n'a pas de période ou de fréquence, par exemple.

Cos graph versus sine graph ?

Quelles sont les similitudes entre les graphiques du cosinus et du sinus ? Eh bien, elles sont assez semblables. Tout d'abord, notez que nous parlons des graphiques de base du cosinus et du sinus, c'est-à-dire sin(x) et cos(x).

Ensuite, le graphique en cos est obtenu en déplaçant simplement le graphique en sinus vers la gauche \(\pi/2\) unités. Ainsi, le graphique en cos et le graphique en sinus sont essentiellement les mêmes, à l'exception d'une translation.

Cos graphique en degrés

Y a-t-il une différence entre le graphique du cosinus en radians et le graphique du cosinus en degrés ? Il y a une différence d'échelle, car le cosinus complète une période complète en \(2\pi\) lorsqu'il est mesuré en radians, alors qu'il complète une période complète en 360° ^o lorsqu'il est mesuré en degrés. Mais en termes de forme, il n'y a pas de différence essentielle.

Comment utiliser cette calculatrice graphique de cos ?

Cette calculatrice de graphique en cos élimine toutes les conjectures, car tout ce que vous avez à faire est de fournir une fonction cos valide. Selon le type de fonction cos que vous fournissez, vous aurez une période, ou peut-être que la période ne sera pas définie, dans un cas comme \(f(x) = cos(x^2)\), où nous disons toujours que nous avons une fonction cos fonction cos .

Les graphiques de Cos, ainsi que les graphiques de sinus et de tangente sont parmi les plus courants graphiques trigonométriques que vous rencontrerez généralement.

Exemple : graphique cos

Calculer le graphique de : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Solution : La fonction suivante a été prévue :

\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\]

Sur la base de l'argument de la fonction trigonométrique qui a été transmis, la fréquence et la période sont calculées comme suit :

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

et aussi

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Par conséquent, en considérant la fonction trigonométrique fournie, \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\), nous obtenons que :

" L'amplitude dans ce cas est \(A = 1/3\).

" Le déphasage est égal à \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

" Le décalage vertical est égal à \( 0\).

En résumé, les résultats suivants ont été obtenus pour la fonction trigonométrique donnée

• Période = \(5.0265\)
• Fréquence = #XYZA
• Amplitude = \(1/3\)
• Décalage de phase = \(0.6667\)
• Décalage vertical = \(\displaystyle 0\)

Voici le graphique correspondant

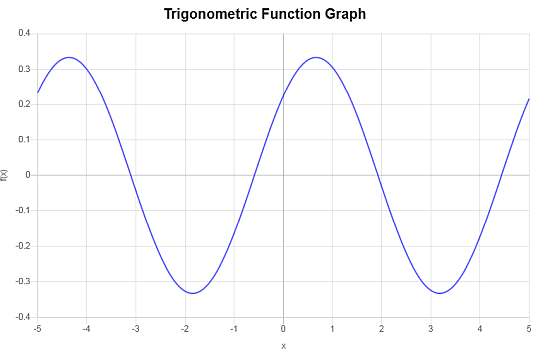
Exemple : autres graphes cos

La fonction suivante est-elle périodique ? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 - \frac{5}{6}\right)\)

Solution : Non, ce n'est pas le cas, à cause du terme \(x^2\).

Exemple : graphique du cosinus

Calculer le graphique de : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Solution : Remarquez que l'expression trigonométrique passée peut être simplifiée comme suit :

la fonction avec laquelle nous allons travailler est donc \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Ainsi, sur la base de l'argument de la fonction trigonométrique passée, la fréquence et la période sont calculées comme suit :

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

et aussi

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

En se basant sur la fonction trigonométrique fournie, \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\), on obtient que :

" L'amplitude dans ce cas est \(A = 2\).

" Le déphasage est égal à \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

" Le décalage vertical est égal à \( 0\).

En résumé, les résultats suivants ont été obtenus pour la fonction trigonométrique donnée

• Période = \(5.0265\)
• Fréquence = #XYZA
• Amplitude = \(2\)
• Décalage de phase = \(0.3667\)
• Décalage vertical = \(\displaystyle 0\)

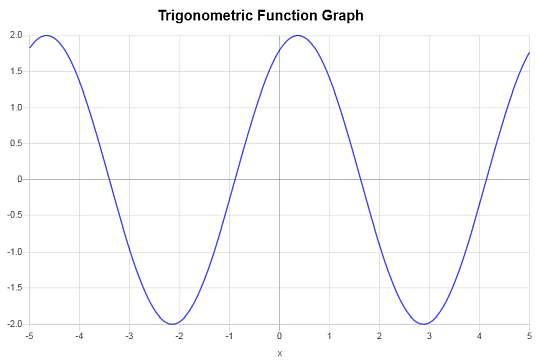
Voici le graphique correspondant

Plus de calculatrices de géométrie

L'une des plus utiles est la suivante calculatrice de période et de fréquence pour cela, vous devez fournir n'importe quelle fonction trigonométrique et vous obtiendrez l'amplitude, la période et la fréquence.

Vous pouvez également utiliser ce calculatrice de sin avec étapes pour travailler avec des expressions trigonométriques plus complexes concernant la fonction sinus. Le sinus et le cosinus sont en effet la pierre angulaire de tout ce qui a trait à la géométrie et à la trigonométrie

Par ailleurs, vous êtes peut-être intéressé par évaluation des expressions trigonométriques ou représentation graphique des fonctions trigonométriques en général.