L'équation du cercle
Un cercle est l'une des figures géométriques les plus remarquables. Il présente une symétrie remarquable, basée sur le fait que TOUS les points du cercle sont équidistants du centre, ce qui signifie en anglais que tous les points du cercle sont à la même distance du centre. Cette distance commune \(r\) s'appelle le rayon du cercle .
Le cercle a de nombreuses applications géométriques importantes, ce qui en fait un objet très important en géométrie et en algèbre.
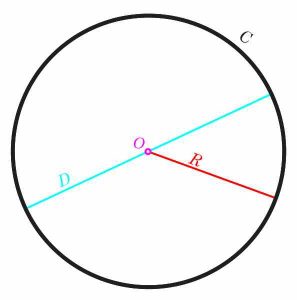
Une autre propriété cruciale du cercle est qu'il est très facilement représentable algébriquement. Cela signifie que nous pouvons facilement établir une équation pour représenter tous les points d'un cercle donné. Pour le dire plus concrètement, considérons le plan de coordonnées \(X - Y\). Tout ce que cela signifie, c'est que nous avons les axes X et Y, qui sont perpendiculaires l'un à l'autre
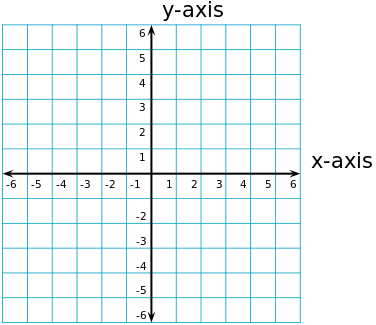
Équation du cercle
Maintenant, parlons de l'équation qui représente tous les points d'un cercle donné. En effet, pour un cercle de rayon \(r\), l'équation suivante décrit les points \((x, y)\) qui sont sur le cercle :
\[\Large x^2 + y^2 = r^2\]Ce qui précède correspond à l'équation d'un cercle de rayon \(r\), dont le centre est situé à \((0,0)\), l'origine des axes de coordonnées.
Quand le rayon est \(r = 1\), alors nous avons ce qu'on appelle un cercle unitaire .
En regardant l'équation ci-dessus, l'interprétation géométrique est que \(x\) et \(y\) sont les côtés d'un triangle et \(r\) est son hypoténuse
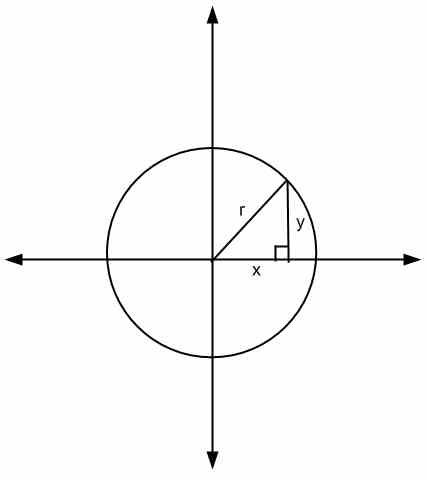
Une autre façon de voir l'équation du cercle est de prendre la racine carrée des deux côtés de l'équation, ainsi nous obtiendrions \(\sqrt{x^2+y^2} = r\), ce qui indique que pour tout point \((x,y)\) sur le cercle, le distance à l'origine (dans ce cas, le centre du cercle) est égal à \(r\).
Equation d'un cercle qui n'est pas centré à l'origine
L'avantage de travailler sur des axes coordonnés est que les points du cercle, et le centre, peuvent être localisé dans les axes, et peut être représenté par une équation, comme indiqué ci-dessus. Mais en général, le centre du cercle n'a pas à être l'origine, il peut être n'importe quel point \((x_0, y_0\) dans les axes coordonnés, dans ce cas, l'équation du cercle devient :
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]qui est connu comme le Equation générale d'un cercle . Par exemple, disons que vous devez calculer l'équation d'un cercle de rayon \(r = 4\), qui est centré au point \((1,2)\). Donc, dans ce cas, nous avons \(x_0 = 1\), \(y_0 = 2\) et \(r = 4\), et ensuite, il suffit de brancher ces nombres dans l'équation ci-dessus et on obtient
\[\large (x-1)^2 + (y-2)^2 = 4^2\]ou on peut aussi écrire
\[\large (x-1)^2 + (y-2)^2 = 16\]Exemple 1
Écrivez l'équation du cercle de rayon 3, dont le centre est à l'origine. À l'aide de cette équation, déterminez si le point (1, 2) appartient ou non au cercle.
Réponse:
Tout d'abord, déterminons l'équation du cercle. Dans ce cas, le cercle est centré à l'origine, donc \((x_0, y_0) = (0, 0)\). Par conséquent, l'équation est
\[\large x^2 + y^2 = 3^2\]qui est identique à
\[\large x^2 + y^2 = 9\]Maintenant, la question est de savoir si le point (1, 2) est sur le cercle ou non. Nous savons que les points sur le cercle seront tels que \(x^2 + y^2 = 9\).
Pour le point \((1, 2)\) on obtient que \(x = 1\) et \(y=2\), donc alors pour ce cas de ce point, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) qui est différent de 9, et donc \((1,2)\) n'appartient pas au cercle.
En savoir plus sur l'équation du cercle
Le cercle est une entité mathématique tellement importante, que des volumes de livres ont été écrits à son sujet. Les cercles traversent la géométrie, la trigonométrie et l'algèbre, c'est pourquoi ils apparaissent de manière transversale partout en mathématiques.
Comment calculer l'équation d'un cercle ?
Lorsque nous travaillons avec un cercle, il y a plusieurs choses à régler. La première chose est de construire l'équation du cercle. Par exemple, considérons un cercle de rayon \(r = 3\), qui est centré sur le point \((1,1)\).
D'après l'équation générale d'un cercle, l'équation est la suivante
\[\large (x-1)^2 + (y-1)^2 = 3^2\]L'équation ci-dessus peut être utilisée, par exemple, pour déterminer si un point appartient ou non au cercle. Que pouvez-vous faire d'autre pour calculer l'équation du cercle ? Vous pouvez éventuellement développer les carrés, de sorte que nous obtenions
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]qui peut être simplifié en
\[\large x^2 - 2x + y^2 -2y = 7\]Ainsi, les deux équations sont équivalentes, dans le sens où elles déterminent le même cercle. Laquelle préférez-vous ? \((x-1)^2 + (y-1)^2 = 3^2\) ou \(x^2 - 2x + y^2 -2y = 7\) ? C'est une question de goût et de ce pour quoi vous utiliseriez la formule.
Aire d'un cercle
Il est intéressant de noter qu'afin de calculer les Aire d'un cercle si vous avez besoin de l'équation complète, vous n'avez pas besoin de l'équation complète, vous avez juste besoin de connaître le rayon. En d'autres termes, le l'aire et la circonférence d'un cercle ne dépendent pas de son centre.
L'équation d'un cercle est-elle une fonction ?
C'est une question que se posent de nombreux étudiants, et nous devons la clarifier. Tout d'abord, le équation du cercle est une équation, et non une relation ou une fonction.
Or, l'équation du cercle détermine une relation, et non une fonction quand on calcule algébriquement résoudre y en fonction de x . En effet, si on résout pour \(y\) on obtient :
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]Cela signifie que pour un \(x\) donné, il y a deux valeurs de \(y\) qui sont associées, qui sont \(\sqrt{ 9 - x^2}\) et \(-\sqrt{ 9 - x^2}\), ce qui indique que l'équation du cercle détermine une relation au lieu d'une fonction.
Un cas spécifique du cercle est le cercle unitaire avec l'équation \(x^2 + y^2 = 1\), qui est centré à l'origine. Le cercle unitaire est particulièrement adapté pour travailler avec expressions trigonométriques d'une manière très visuelle.
