Calcul de l'élasticité-prix de la demande à partir de données d'échantillon

Utilisez cette calculatrice pour estimer l'élasticité-prix de la demande en fonction des données d'échantillon pour le prix et la quantité demandés que vous fournissez.

Vous devrez fournir des données d'échantillon valides, en termes de valeurs positives pour les deux échantillons (prix et quantité demandée). Une fois vos données collées dans la feuille de calcul, vous pouvez cliquer sur « Calculer » pour obtenir toutes les étapes affichées.

Notez que cette approche nécessite que les données suivent un modèle spécifique qui convient à un modèle log-log, où \(\ln(P)\) et \(\ln(Q)\) sont utilisés comme variables auxiliaires pour mener un modèle de régression linéaire.

Calcul de l'élasticité des prix à partir de données d'échantillon

Afin de calculer l'élasticité des prix, vous devrez estimer le modèle auxiliaire suivant :

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Notez que cela correspond à un modèle de régression linéaire régulier dans lequel les variables d'origine, prix et quantité, sont transformées en logarithme. C'est pourquoi nous exigeons que les deux variables soient strictement positives.

Quelles sont les étapes pour calculer l'élasticité ?

• Étape 1 : Identifier les données d'échantillon pour les variables fournies pour le prix (P) et la quantité (Q)
• Étape 2 : Assurez-vous que les deux échantillons ont la taille d'échantillon d'échantillon et qu'ils sont TOUS DEUX positifs, sinon vous ne pourrez pas faire le calcul
• Étape 3 : Transformation logarithmique des deux variables : calcul de ln(X) et ln(Y)
• Étape 4 : Effectuer une régression linéaire auxiliaire pour les variables ln(X) et ln(Y), où ln(X) est la variable indépendante et ln(Y) est la variable dépendante
• Étape 5 : Le coefficient de pente trouvé pour cette régression auxiliaire est l'élasticité-prix de la demande pour ces données

L’étape cruciale est alors la transformation logarithmique des données, qui nous permet de calculer l’élasticité sur la base des résultats d’une régression linéaire, rendant les résultats trouvés hautement interprétables.

Comprendre l'élasticité des prix

Par définition, l'élasticité des prix est définie à l'aide de la formule suivante :

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Cela indique, entre autres, que nous pouvons prédire le pourcentage de variation de la demande quantitative à l'aide de l'expression suivante :

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Cela indique que le pourcentage de variation de Q est le même que le pourcentage de variation de P multiplié par l'élasticité. Il est important de noter que cette définition s'applique ponctuellement : cela signifie que l'élasticité ne doit pas nécessairement être constante tout au long de la courbe de demande. Bien que cela soit possible, et dans cette calculatrice, une telle hypothèse est faite.

Interprétation des coefficients d'élasticité des prix

Comme nous l'avons vu dans la section précédente, l'élasticité \(\varepsilon\) correspond simplement au coefficient de pente de la régression auxiliaire log-transformée. Mais elle a aussi une interprétation de changement marginal très intéressante :

• Pour une variation supplémentaire de 1 % du prix, la quantité demandée change de \(\varepsilon \%\)

C'est précisément ce que requiert et implique la formule d'élasticité. Notez que ce calculateur estime un modèle qui suppose que les données suivent un modèle propice à une élasticité constante, ce qui n'est pas le cas pour une fonction de demande linéaire, par exemple.

Facteurs influençant l'élasticité des prix

L'élasticité reflète la réaction des consommateurs aux variations de prix. En général, l'élasticité est négative : si le prix d'un bien augmente, l'acheteur achètera probablement moins, du moins s'il s'agit d'un bien normal.

Une élasticité supérieure à 1 en valeur absolue (inférieure à -1) est dite associée à une réaction élastique au prix, tandis qu'une élasticité comprise entre 0 et 1 en valeur absolue (entre -1 et 0) est dite associée à une réaction inélastique au prix.

La théorie économique prédit que différents facteurs peuvent affecter l'élasticité-prix de la demande. Par exemple, l'absence ou la pénurie de substituts entraînera une plus grande élasticité en valeur absolue.

Exemple de calcul d'élasticité : utilisation de données d'échantillon

Calculez l'élasticité à partir des données d'échantillon suivantes :

P	Q
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

La Solution :Afin de trouver l'élasticité-prix de la demande à partir de ces données, nous devons construire un modèle de régression log-log, où la variable indépendante que nous utiliserons est \(ln(P)\), et la variable dépendante est le logarithme naturel de \(ln(Q)\)

Afin de calculer les coefficients de régression pour cette régression auxiliaire, le tableau suivant doit être utilisé :

	P	Z = ln(P)	Q	W = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

Sur la base du tableau ci-dessus, les éléments suivants sont calculés :

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Par conséquent, sur la base des calculs ci-dessus, les coefficients de régression (la pente \(m\) et l'ordonnée à l'origine \(n\)) sont obtenus comme suit :

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Par conséquent, nous constatons que l’équation de régression est :

\[W = 2.1639 + 0.715 \text{ Z}\]

Mais comme les variables auxiliaires sont \(Z = \ln(X)\) et \(W = \ln(Y)\), nous concluons que l'équation de régression log-log est :

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Par conséquent, sur la base des informations fournies ci-dessus, le diagramme de dispersion et le diagramme de régression suivants sont obtenus :

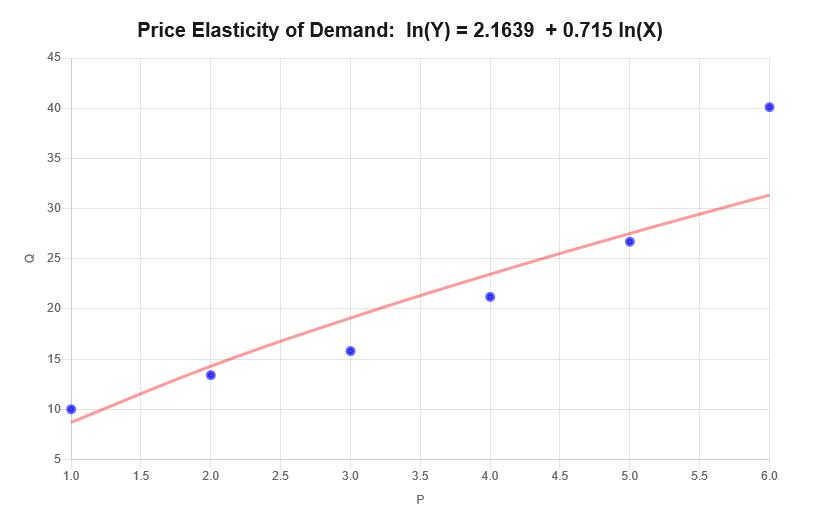
Interprétation

L'élasticité dans ce cas correspond au coefficient de pente des données fournies, ce qui signifie que \(\varepsilon = 0.715 \), ce qui peut être interprété comme suit :

• Pour une augmentation de 1% du prix, il y a une augmentation moyenne de 0,715% de la quantité demandée.

Des calculatrices plus intéressantes

L'estimation de modèles à partir de données d'échantillons est une compétence essentielle nécessaire à la fois en statistique et en économie. L'utilisation de données d'échantillons pour calculer un modèle de régression est l’une des applications les plus courantes de l’utilisation de données d’échantillon pour la création de modèles.

Mais il arrive souvent qu'un modèle linéaire régulier ne s'adapte pas suffisamment bien aux données, et pour cela nous devons essayer différentes structures fonctionnelles. Par exemple, nous pourrions potentiellement estimer un Régression log-log , un régression logarithmique ou un Régression polynomiale , pour n’en citer que quelques-unes, qui pourraient être plus efficaces que la régression classique pour expliquer la variation de la variable dépendante.

L'option de calcul de l'élasticité à partir de données d'échantillon est principalement utilisé dans un cadre exploratoire. Le plus souvent, le l'élasticité est directement calculée à partir de la fonction de demande , lorsqu'elle est disponible. Dans d'autres circonstances, l'élasticité est estimée à partir d'une paire de points de prix-demande en utilisant la formule d'élasticité de l'arc .