Comment fonctionne un calculateur de régression logarithmique

Cette calculatrice vous permettra d'estimer une régression logarithmique pour les données d'échantillon que vous fournissez dans la feuille de calcul de saisie de données correspondante.

Lorsque des données valides sont fournies (dans ce cas, la variable X ne peut prendre que des valeurs positives), après avoir cliqué sur « Calculer », vous obtiendrez un aperçu des étapes impliquées dans le processus ainsi qu'un nuage de points qui montrera la qualité de l'ajustement.

Notez que lorsque les données sont dimensionnellement valides, vous pouvez toujours exécuter une régression logarithmique, mais cela ne signifie pas que les résultats seront de bonne qualité, du moins en termes d'ajustement.

Outils et calculatrices pour la régression logarithmique

Il existe différents outils que vous pouvez utiliser pour estimer votre régression logarithmique. En théorie, vous pouvez procéder manuellement, en utilisant une transformation logarithmique à l'aide d'une calculatrice ordinaire peut-être (même celles fournies avec votre téléphone), puis utiliser une équation auxiliaire des moindres carrés pour trouver le modèle logarithmique, qui est

\[ Y = a + b \ln(X) + \varepsilon \]

Certes, l'approche manuelle peut être fastidieuse et sujette aux erreurs, c'est le moins qu'on puisse dire. C'est pourquoi c'est une très bonne option d'utiliser cette méthode Calculateur de régression logarithmique , car il fait tout le travail pour vous et vous montre toutes les étapes

Il existe d'autres outils comme les applications pour téléphones mobiles qui sont censés effectuer tous les types de régression, mais vous devrez essayer et voir car cela pourrait être une situation aléatoire.

Étapes pour exécuter une régression logarithmique

• Étape 1 : Énumérez clairement la variable indépendante (X) et la variable dépendante (Y) et assurez-vous que les deux variables ont la même taille d'échantillon
• Étape 2 : Assurez-vous que vos valeurs de X sont positives, sinon vous ne pouvez pas exécuter la régression
• Étape 3 : Construire une nouvelle variable indépendante X* = ln(X) en appliquant la transformation du logarithme naturel
• Étape 4 : Vous exécutez maintenant une analyse de régression linéaire régulière pour X* par rapport à Y

Une chose à garder à l'esprit est qu'il est tout à fait conseillé d'utiliser une calculatrice ou un logiciel afin d'obtenir des statistiques de diagnostic qui vous aideront à évaluer s'il est judicieux ou non d'utiliser le modèle de régression logarithmique .

Utilisation d'excel et de calculatrices de régression logarithmique dédiées

Excel joue un rôle important en vous aidant à effectuer des analyses statistiques de base : il vous fournit une interface claire et éprouvée pour exécuter des tests de base, y compris le calcul de la régression logarithmique.

Le principal problème d'Excel est qu'il ne vous fournit pas l'étape de résolution. Cela pourrait aider avec l'avènement de cadres d'IA tels que Copilot, qui doteraient probablement Excel d'étapes descriptives du calcul.

Comprendre et interpréter les résultats du calculateur de régression

Comme tout autre Analyse de régression , pour le cas logarithmique, ce n'est pas différent dans la mesure où vous examinerez les statistiques d'ajustement du modèle, telles que Statistique F pour tester la signification du modèle dans son ensemble, et t-statistiques pour la signification individuelle des prédicteurs .

De plus, vous voudrez probablement jeter un œil aux variations et aux erreurs expliquées, ainsi qu'aux Coefficients R^2 et R^2 ajusté , qui vous fournira des estimations de la variation expliquée de la variable dépendante par le modèle.

Exemples de régression logarithmique

Tenez compte des variables

X: 1, 2, 3, 4, 5

Et : 15, 25, 28, 29, 30

Estimez un modèle de régression logarithmique.

Solution :

Les données suivantes pour les variables X et Y sont fournies pour construire un modèle de régression logarithmique :

X	Y
1	15
2	25
3	28
4	29
5	30

La variable indépendante que nous utiliserons est le logarithme naturel de X, et la variable dépendante est Y. Afin de calculer les coefficients de régression pour cette régression auxiliaire, le tableau suivant doit être utilisé :

	X	Z = ln(X)	Y	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

Sur la base du tableau ci-dessus, les éléments suivants sont calculés :

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Par conséquent, sur la base des calculs ci-dessus, les coefficients de régression (la pente \(m\) et l'ordonnée à l'origine \(n\)) sont obtenus comme suit :

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Par conséquent, nous constatons que l’équation de régression est :

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Mais puisque la variable auxiliaire \(Z = \ln(X)\), nous concluons que l'équation de régression logarithmique est :

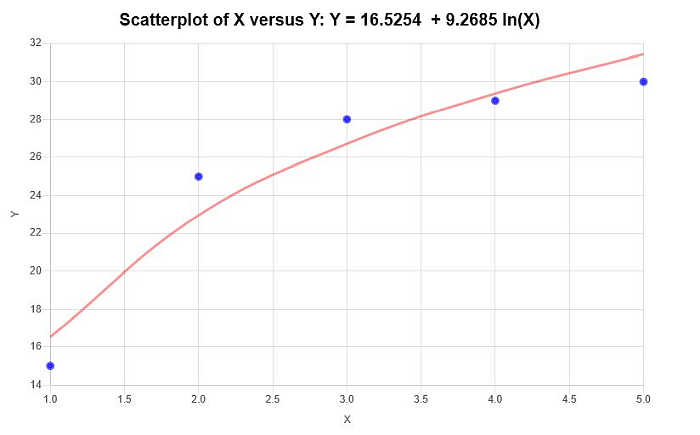
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Par conséquent, sur la base des informations fournies ci-dessus, le diagramme de dispersion et le diagramme de régression suivants sont obtenus :

Plus de calculatrices de statistiques

Vous pouvez également être intéressé par calculer une régression exponentielle , ou élaborer les subtilités d'un Régression polynomiale , qui s’appliquent tous dans des contextes différents, en fonction du comportement des données d’échantillon observées.

Il est probable que vous souhaitiez construire un diagramme de dispersion afin d'évaluer le comportement empirique des données et de pré-évaluer si une régression logarithmique s'applique au lieu d'un autre type de régression.