Question 1: Les formules pour la ligne des moindres carrés ont été trouvées en résolvant le système d'équations

\[nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

Résolvez ces équations pour b et m pour montrer que

\[\begin{align} & m=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left(\sum{{{x}^{2}}} \right)-{{\left( \sum{x} \right)}^{2}}} \\ & b=\frac{\sum{y-m\left( \sum{x}\right)}}{n} \\ \end{align}\]

Solution: De

\[ nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

nous avons deux équations et deux inconnues (m et b)

Nous obtenons cela en multipliant la première équation par \(\left( \sum{x} \right)\) et la seconde par -n nous obtenons

\[\begin{align} & nb\left( \sum{x} \right)+m{{\left( \sum{x} \right)}^{2}}=\left( \sum{y}\right)\left(\sum{x} \right) \\ & -nb\left( \sum{x} \right)-mn\left( {{\sum{x}}^{2}}\right)=n\sum{xy} \\ \end{align}\]

et maintenant en ajoutant ceux-ci:

\[m\left( {{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right) \right)=\left( \sum{x} \right)\left(\sum{y} \right)-n\left( \sum{xy} \right)\]

\[\Rightarrow \,\,\,\,m=\frac{\left( \sum{x} \right)\left( \sum{y} \right)-n\left( \sum{xy} \right)}{{{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right)}=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left( {{\sum{x}}^{2}} \right)-{{\left( \sum{x} \right)}^{2}}}\]

Maintenant, à partir de cette équation:

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\]

nous pouvons résoudre pour b :

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\,\,\Rightarrow \,\,\,nb=\left( \sum{y} \right)-m\left( \sum{x} \right)\,\Rightarrow \,\,\,b=\frac{\left( \sum{y} \right)-m\left( \sum{x} \right)}{n}\]

Question 2: Déterminez le coefficient de corrélation et tracez un graphique de la droite de régression avec le coefficient de régression pour l'ensemble de données suivant.

Incendies de forêt et hectares brûlés. Le nombre d'incendies et le nombre d'acres brûlés sont les suivants

Incendies (x)	72	69	58	47	84	62	57	45
Acres (y)	62	41	19	26	51	15	30	15

Solution: (a) Le nuage de points suivant est obtenu:

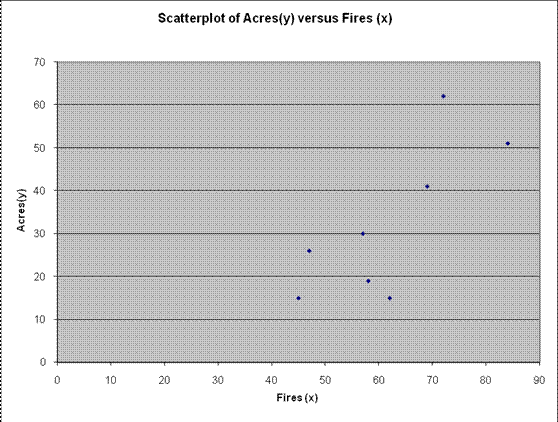
Sur la base du nuage de points ci-dessus, nous observons qu'il existe un degré modéré à fort d'association linéaire positive.

(b) D'autre part, nous avons le tableau suivant qui montre les calculs nécessaires pour calculer la corrélation de Pearson: Nous obtenons

La corrélation de Pearson r est calculée comme

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {17216}-{494}\times {259}}{\sqrt{8\times {31692}-{494}^{2}}\sqrt{8\times 10513-{259}^{2}}}\]

\[=0.7692\]

(c) Le coefficient de détermination est

\[{{r}^{2}}={0.7692}^{2}= {0.5917}\]

ce qui signifie que 59,17% de la variation en Acres (y) est expliquée par Fires (x).

(d) Les coefficients de régression sont calculés

\[b=\frac{n\left( \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \right)-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}=\frac{8 \times {17216}-{494}\times {259}}{8 \times {31692}-{494}^{2}}= 1.0297\]

and

\[a=\bar{y}-b \bar{x}={32.375}{+} {1.0297}\,\cdot \, {61.75} = {-31.208}\]

Cela signifie que l'équation de régression est

\[\hat{y}= {-31.208}{+}{1.0297}\,x\]

Graphically:

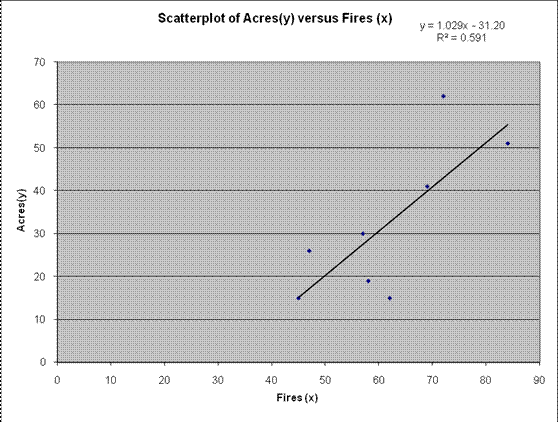
Question 3: Vous avez mené une étude pour déterminer si le temps moyen passé dans le laboratoire d'informatique chaque semaine et la note du cours dans un cours d'informatique étaient corrélés. En utilisant les données ci-dessous, quelle conclusion tireriez-vous sur cette question?

student	# hours in lab	Course Grade
1	20	96
2	11	51
3	16	62
4	13	58
5	89
6	15	81
7	10	46
8	10	51

Solution: Le tableau suivant montre les calculs nécessaires pour calculer Pearson corrélation r : On a

La corrélation de Pearson r est évalué comme

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {7925}-{112}\times {534}}{\sqrt{8\times {1660}-{112}^{2}}\sqrt{8\times 38224-{534}^{2}}}\]

\[=0.9217\]

Nous voulons tester la signification du coefficient de corrélation. Plus précisément, nous voulons tester

\[\begin{align}{{H}_{0}}:\rho {=} 0 \\ {{H}_{A}}:\rho {\ne} 0 \\ \end{align}\]

Afin de tester l'hypothèse nulle, nous utilisons un test t. La statistique t est organisée comme

\[t= r \sqrt{\frac{n-2}{1-{{r}^{2}}}}= {0.9217} \times \sqrt{\frac{6}{1-{0.9217}^2}}= {5.8198}\]

La valeur p bilatérale pour ce test est évalué comme

\[p=\Pr \left( |{{t}_{6}}|>5.8198 \right)=0.0011\]

Depuis \(p = 0.0011 {<} 0.05\) , et cela signifie que nous rejetons l'hypothèse nulle H ₀ .

Par conséquent, nous avons suffisamment de preuves pour soutenir l'affirmation selon laquelle la corrélation entre le nombre d'heures en laboratoire et la note du cours est significativement différente de zéro.