Reglas de exponentes
Las operaciones con exponentes se encuentran entre las operaciones más comunes que realizará en matemáticas, y es crucial que tenga una base adecuada sobre ellas.
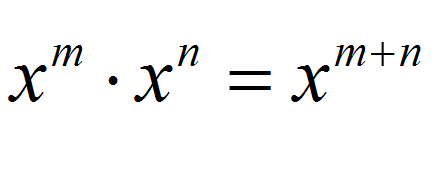
Sin más preámbulos, enumeremos las propiedades básicas del exponente. Usar estas propiedades de manera competente es de suma importancia. Las reglas son:
Regla 1: \(\large \displaystyle x^0 = 1\), para \(x = \not 0\)
Regla 2: \(\large\displaystyle x^1 = x\)
Regla 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regla 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regla 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Regla 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Te explicamos un poco estas reglas en palabras .
Regla 1
está diciendo que cualquier cosa elevada a la potencia de cero es igual a 1. Bueno, excepto por 0, porque por convención (y hay una buena razón para ello) \(0^0 = 0\).
Ahora,
Regla 2
está diciendo que tomar cualquier número y elevarlo a la potencia de 1 da el mismo número original. En otras palabras, elevar un número a la potencia de 1 no afecta el número.
Regla 3
Está diciendo que cuando multiplico potencias con la misma base, el resultado es una potencia que tiene la misma base, elevado a una potencia que corresponde a la suma de los exponentes de las potencias que estoy multiplicando.
Regla 4
está diciendo que tomar la potencia de una potencia es lo mismo que tomar una potencia con los exponentes multiplicados como exponente.
Regla 5
Está diciendo que cuando divido potencias con la misma base, el resultado es una potencia que tiene la misma base, elevado a una potencia que corresponde a la resta de los exponentes de las potencias que estoy multiplicando.
Regla 6
está diciendo que cuando tengo una potencia que afecta a una multiplicación, es lo mismo que multiplicar cada uno de los términos elevados a esa potencia.
EJEMPLO 1
Simplifica la siguiente expresión
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]RESPONDER:
Usando la Regla 5 para la división de poderes con la misma base:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]¿Debería preocuparme por los exponentes negativos?
Realmente no. En primer lugar, las 5 reglas para los exponentes mencionadas anteriormente no establecen ninguna afirmación específica sobre que los exponentes deben ser no negativos. De hecho, las reglas funcionan igual si los exponentes son negativos.
De hecho, para exponentes negativos , habrá dos reglas que te permitirán transformarlas en exponentes positivos:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
Esta expresión anterior nos muestra que podemos convertir una potencia con un exponente negativo que está en el numerador en una potencia en el denominador con el correspondiente exponente positivo.
Esta expresión anterior nos muestra que podemos convertir una potencia con un exponente negativo que está en el denominador en una potencia en el numerador con el correspondiente exponente positivo.
EJEMPLO 2
Simplifique la siguiente expresión, sin dejar exponentes negativos:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]RESPONDER:
Transformar los exponentes negativos en exponentes positivos y aplicar las reglas de los 5 exponentes:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]que concluye la simplificación.
¿Están estas reglas de exponente relacionadas de alguna manera con las reglas de los logaritmos?
¡Absolutamente! Revisar la reglas logarítmicas y descubrirá que son estructuralmente muy similares, y esto se debe a que los logaritmos y las potencias son operaciones inversas entre sí.
Solo como una pequeña muestra, hagamos una prueba rápida. Suponga que \(a = x^m\) y \(b = x^n\). Luego, por definición, \(m = \log_x a\) y \(n = \log_x b\). Entonces, según las reglas del exponente, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Por lo tanto, por definición, \(m + n = \log_x (a \cdot b)\). Pero \(m = \log_x a\) y \(n = \log_x b\), entonces \(\log_x a + \log_x b = \log_x (a \cdot b)\).
Más sobre la regla de los exponentes
Una cosa en la que debemos enfatizar es en el hecho de que las reglas para exponentes no requieren que los exponentes sean positivos. No es necesario que los exponentes sean números enteros. Las reglas son válidas para exponentes reales.
• No olvides que si estás tratando con un exponente negativo en el numerador, puedes transformarlo pasándolo al denominador con exponente positivo.
• Además, si está tratando con un exponente negativo en el denominador, puede transformarlo pasándolo al numerador con exponente positivo.
Las reglas de los exponentes tienen muchas aplicaciones, incluida la provisión de una base para obtener la reglas para simplificar radicales , que vienen como corolario de las raíces de exponentes.
En términos gráficos, puede explorar esta regla mediante graficar diferentes funciones exponenciales y ver las propiedades específicas que tienen.