Operaciones con exponentes negativos
Las operaciones con exponentes se encuentran entre las operaciones más fundamentales en Álgebra, y entre ellas, las que involucran exponentes negativos son las que traen más complicaciones a los estudiantes.
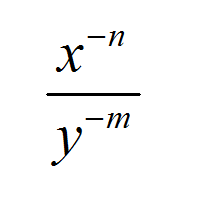
Primero, recordemos las propiedades básicas del exponente. El uso de estas propiedades es omnipresente en la mayoría de las áreas de las matemáticas. Las reglas son:
Regla 1: \(\large \displaystyle x^0 = 1\), para \(x = \not 0\)
Regla 2: \(\large\displaystyle x^1 = x\)
Regla 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regla 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regla 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Por ejemplo, cuando tienes una expresión como \(3^5 \cdot 3^7\), sabemos que usamos la regla de multiplicación (Regla 3) para obtener:
\[\large 3^5 \cdot 3^7 = 3^{5+7} = 3^{12}\]Las reglas de los exponentes: ¿Qué sucede con los exponentes negativos?
Incluso si no te diste cuenta, las reglas anteriores no dicen que los exponentes deben ser positivos. De hecho, podrían ser negativos y las reglas también se mantendrán.
Ahora, de las Reglas 1 y 5 podemos derivar la relación entre exponentes positivos y negativos. Entonces, para la Regla 5, asuma que \(m = 0\) y \(n\) es positivo. Entonces, obtenemos
\[\large\displaystyle \frac{1}{x^n} = \frac{x^0}{x^n} = x^{0-n} = x^{-n}\]La expresión anterior nos da una relación simple entre exponentes positivos y negativos:
\[\large\displaystyle \boxed{\frac{1}{x^n} = x^{-n}}\]
Esta expresión anterior nos dice que podemos pasar una potencia con un exponente negativo en el numerador al denominador con el correspondiente exponente positivo. Esta es una 'regla' de exponentes negativos
La belleza de la fórmula anterior es que podemos multiplicar de forma cruzada los términos en ambos lados de la igualdad, y podemos escribir la expresión anterior en una forma ligeramente diferente:
\[\large\displaystyle \boxed{\frac{1}{x^{-n}} = x^{n}}\]
Esta última expresión suele ser muy útil, porque nos está diciendo que podemos llevar una potencia con exponente negativo en el denominador al numerador pero con el correspondiente exponente positivo. Esto puede considerarse como otra "regla" para exponentes negativos.
EJEMPLO 1
Simplifique la siguiente expresión y déjela sin exponentes negativos:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2}\]RESPONDER:
Usando la regla de los exponentes negativos, cambiamos exponentes positivos / negativos entre numerador / denominador:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2} = \frac{x^{3}\sqrt{x} x^{1/2}}{ y^2 y^{3}}\] \[\large = \frac{x^{3} x^{1/2} x^{1/2}}{ y^2 y^3} = \frac{x^{3+1/2+1/2}}{ y^{2+3}} \] \[\large = \frac{x^{4}}{ y^{5}} \]y terminamos con la simplificación, porque no queda nada por simplificar.
Más sobre exponentes negativos
Una de las conclusiones más importantes de este tutorial sobre exponentes negativos es que tenemos reglas para convertir esos exponentes negativos en exponentes positivos. ¿Como hacemos eso?
• Si tenemos un exponente negativo en el numerador (por lo que está multiplicando por un exponente negativo), podemos pasarlo al denominador con exponente positivo.
• Si tenemos un exponente negativo en el denominador (entonces estás dividiendo por un exponente negativo), podemos pasarlo al numerador con exponente positivo.
Operar con exponentes negativos es solo una pequeña parte del tema de lidiar con reglas de exponentes , que le dan una idea clara de por qué el caso con exponentes negativos funciona de la manera en que lo hace.