Reglas de registro
La función logarítmica es una de las funciones más importantes en matemáticas, y las reglas de registro son simples y convenientes, lo que hace que sea realmente fácil trabajar con logaritmos.
Primero recordemos cuál es el significado de \(\log_b a\). En este contexto, el valor \(b\) es el base del logaritmo, y \(a\) es el argumento .
Decimos que \(\log_b a = y\) cuando \(b^y = a\). Esto quiere decir que \(\log_b a\) es el número al que debe elevarse \(b\) (la base) para obtener \(a\) (el argumento).
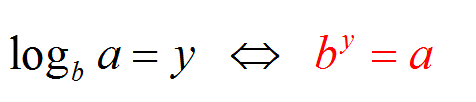
Por ejemplo, \(\log_{10} 25\) corresponde al número al que necesito subir 10 para obtener 25. Entonces, el logaritmo que estoy buscando es el número \(y\) que tiene la propiedad que \(10^y = 25\)
Ahora la pregunta es, ¿cómo calculamos ese número \(y\) que tiene la propiedad \(10^y = 25\)? Bueno, ese número está bien definido y la función logarítmica \(f(x) = \log_{10} x\) se encarga de ello. Esta función no es una función elemental y se necesita una serie de Taylor (serie infinita) para representarla.
O puede usar una calculadora (que probablemente sea más fácil, ¿verdad?).
Reglas logarítmicas: propiedades de los logaritmos
Estas son las principales reglas de registro:
Regla 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Regla # 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Regla # 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Regla # 4 : \(\large \log_a (a) = 1 \)
Regla # 5 : \(\large \log_a (1) = 0 \)
EJEMPLO 1
Simplifique \(\log_2 8 + \log_2 4\) usando Reglas de registro:
RESPONDEDOR:
Usando la Regla # 1, encontramos que:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Entonces, el primer paso es una aplicación simple de la Regla # 1, pero ¿cómo obtenemos ese \(\log_2 32 = 5\)? Es porque \(2^5 = 32\), entonces en este caso encontramos directamente cuál es el número que necesita aumentar \(2\) para obtener \(32\).
La mayoría de los logaritmos necesitará una calculadora para calcularlos. Son solo unos pocos seleccionados los que pueden calcular directamente. Cosas como \(\log_{10} 100 = 2\), porque sabes fácilmente que \(10^2 = 100\).
Pero, ¿puedes calcular \(\log_{10} 102\) directamente? Realmente no, necesitas una calculadora para eso.
EJEMPLO 2
Exprese a la suma y resta de logaritmos: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
RESPONDEDOR:
En primer lugar, debemos recordar que tomar una raíz cúbica equivale a elevar a la potencia \(1/3\). En otras palabras, \(\sqrt[3]{x}\) es lo mismo que \(x^{1/3}\).
Entonces, primero usamos la Regla # 3 para poner la potencia delante del logaritmo, y luego usamos las Reglas # 1 y # 2. Obtenemos:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]que es lo que se requería: suma y resta de logaritmos simples.
La fórmula de cambio de base para logaritmos
Una de las fórmulas más útiles relacionadas con los logaritmos es la fórmula de cambio de base. Esta fórmula es la siguiente:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Esta fórmula solo dice que si desea cambiar la base de \(b\) a \(c\), los resultados son los mismos, pero debe dividir por el logaritmo de la nueva base.
Ahora, si tiene una orientación artística, puede disfrutar de la forma alternativa del cambio de fórmula basada que se expresa a continuación:
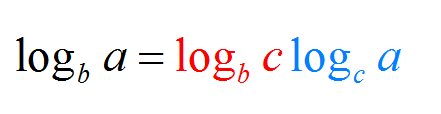
EJEMPLO 3
Exprese el logaritmo natural \(\ln\) en términos de \(\log\) (base 10).
RESPONDEDOR:
Usando la fórmula de cambio de base, obtenemos que:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Entonces estás diciendo que \(\ln a\) se obtiene dividiendo \(\log a\) por \(\log e\). ¿Que conveniente? ¿Quién dice que las matemáticas fueron difíciles, eh?
Más sobre las reglas de registro
Los logaritmos son realmente importantes en matemáticas. Históricamente, los logaritmos juegan un papel muy importante en Astronomía, como una forma de predecir el movimiento de la luna y los planetas.
Las funciones logarítmicas se encuentran en el medio de todo en matemáticas, se entrelazan con exponenciales, exponentes y prácticamente todo. Por eso te piden que te aprendas los logaritmos de memoria, porque son importantes.
Además, estas reglas de registro presentadas aquí juegan un papel crucial para facilitar la resolución de ecuaciones logarítmicas .
Convenciones de notación
Hay un par de convenciones de notación que debe conocer. En general, escribimos \(\log_b a\), y lo decimos "log base b of a". Cuando la base es \(b = 10\), por convención simplemente escribimos \(\log a\). Entonces, cuando ve un \(\log\) sin una base, se asume que la base es \(10\).
Hay otro caso notable. Para \(\log_b a\), cuando la base es \(b = e\) (la constante de Euler), escribimos \(\ln a\) en lugar de \(\log_e a\). Entonces, cuando se usa \(\ln\) en lugar de \(\log\), es porque la base del logaritmo es \(e\).
Observe que \(\ln a\) generalmente se conoce como el tronco natural . Y sí, los registros naturales tienen las mismas reglas que el registro general.
Si tiene una función logarítmica que le gustaría graficar, puede probar nuestra Creador de gráficos de funciones logarítmicas , que le proporcionará un gráfico perfectamente presentado.
