La parábola
Una parábola es el lugar geométrico de puntos en los ejes de coordenadas que tienen la propiedad de ser equidistantes de un punto fijo (llamado foco) y una línea (llamada directriz).
Sé lo que suena un poco demasiado técnico, pero lo repasaremos, y al final verán que no es tan difícil.
Entonces, ¿ayudaría si le dijera que
la función \(f(x) = x^2\) representa una parábola?
Seguro que te ayudará. Y puede que estés pensando "¿por qué no me dijiste desde el principio que la parábola es esa función?".
Como no hay una parábola, hay un número infinito de ellos. Y una parábola ni siquiera tiene que estar representada por una función. Sí, algunas relaciones son parábolas, como veremos.
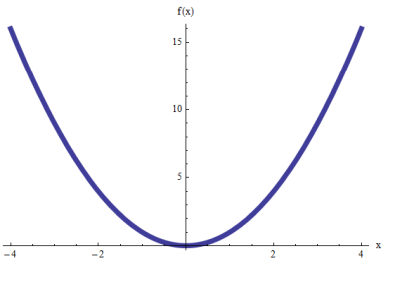
Una cosa es importante mencionar: al usar funciones y relaciones, están las parábolas que se "abren" a lo largo del eje x, y están las parábolas que se "abren" a lo largo del eje y.
Al final, por simetría, es fácil darse cuenta de que esas parábolas que se "abren" a lo largo del eje y tienen la misma estructura que las que se "abren" a lo largo del eje x, por lo que basta con aprender a manejar un tipo.
La ecuación general de la parábola
Hay derivaciones simples para obtener la ecuación de una parábola basada en la ubicación de una directriz y el foco, pero omitiremos la derivación en esta introducción.
Consulte el gráfico a continuación. Necesitamos identificar algunos elementos cruciales de la parábola: tenemos el vértice, el foco y la directriz.
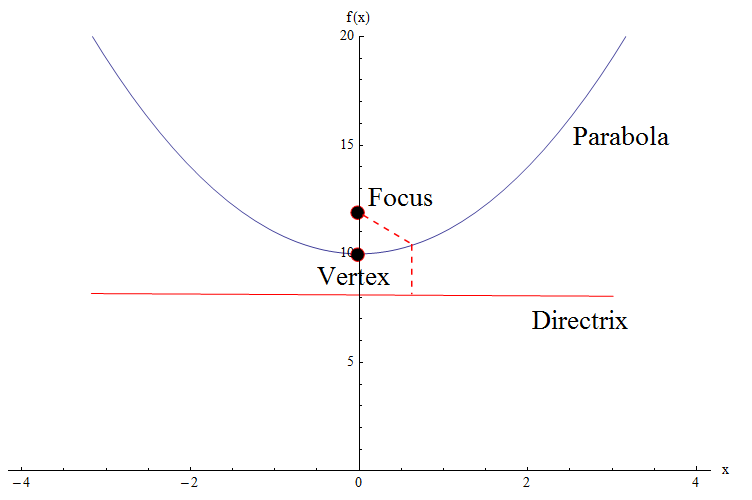
No entraremos en muchos detalles, pero diremos que la ecuación de una parábola general con vértice en el origen, con foco \((0, a)\) y directriz igual a \(y = -a\) es
Esta parábola es el tipo de parábola que se abre a lo largo del eje y.
Ahora, ¿qué sucede cuando en lugar de tener el vértice en el origen, queremos tener el vértice en un punto dado \((k,h)\)?
Bueno, esa es la magia de trabajar con un sistema de coordenadas, ¿y todo lo que necesitamos para hacer una traslación por el punto \((k,h)\)? Pero, ¿cómo se hace una traducción de \((k,h)\)?
¡Sencillo! Donde sea que tenga \(x\), lo reemplace por \(x-k\), y donde tenga \(y\), lo reemplace por \(x-h\).
Por lo tanto, haciendo una traslación, la ecuación de una parábola general con vértice en el punto \((k,h)\), con foco \((k, h+a)\) y directriz igual a \(y = h-a\) es
\[\large y-h = 4a(x-k)^2\]que se puede escribir como
\[\large \boxed{ y = 4a(x-k)^2 + h }\]¿Qué sucede con las parábolas que se abren a lo largo del eje x?
Por simetría, esto simplemente se obtiene reemplazando los roles de \(x\) y \(y\) en la ecuación de la parábola que ya tenemos. En la práctica, esto significa que dondequiera que aparezca \(x\) en la ecuación de la parábola que tenemos, lo cambiamos \(y\), y viceversa por \(y\).
Por tanto, la ecuación de una parábola general con vértice en el punto \((h,k)\), con foco \((h+a, k)\) y directriz igual a \(x = h-a\) es:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Note la diferencia:
Cuando una parábola tiene una directriz de la forma \(y = -a\), entonces la parábola se abre a lo largo del eje y (hacia arriba o hacia abajo dependiendo de si el foco está por encima o por debajo de la directriz).
Cuando una parábola tiene una directriz de la forma \(x = -a\), entonces la parábola se abre a lo largo del eje x (izquierda o derecha dependiendo de si el foco está a la izquierda o derecha de la directriz).
EJEMPLO 1
Encuentra la ecuación de la parábola que tiene una directriz \(y = -4\) y un foco \((0, 4)\). También encuentra el vértice.
RESPONDER:
El vértice está en la parábola, por lo que es equidistante de la directriz \(y = -4\) y el foco \((0, 4)\), entonces el vértice es \(0, 0)\). Por otro lado, para una parábola con vértice en el origen, la ecuación de la directriz es \(y = -a\), entonces en este caso \(a = 4\). En consecuencia, la ecuación de la parábola es
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Gráficamente:
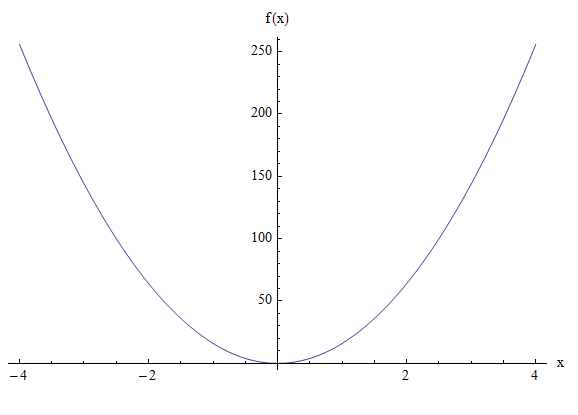
EJEMPLO 2
Encuentra el vértice, el foco y la directriz de la parábola \(y = 8x^2 - 16x + 9\).
RESPONDER:
Primero que nada, necesitamos completar el cuadrado:
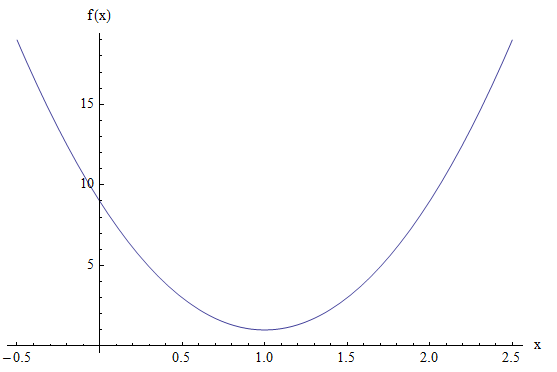
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]Al equiparar esto con la ecuación general, encontramos que el vértice está en el punto \((1, 1)\), y también tenemos ese \(4a = 8\), entonces \(a = 2\), por lo tanto, la directriz es \(y = h - a = 1 - 2 = -1\) y el foco es \((k, h + a) = (1, 1+2) = (1, 3)\).
Gráficamente:
La parábola y las secciones cónicas generales
Por extraño que parezca, la parábola está estrechamente relacionada con el cono. ¿Como dirias? Un matemático griego llamado Apolonio tiene el mérito de haber contribuido con la versión moderna, utilizando sistemas de coordenadas, de las secciones cónicas.
Apolonio y otros matemáticos descubrieron que cuando se corta un cono con un plano, dependiendo del ángulo relativo del cono y del plano, el cono se corta de tal manera que la sección tiene diferentes formas.
Las diferentes formas de las secciones, dependiendo del ángulo de corte relativo, son lo que conocemos como parábola, círculo, elipse e hipérbola, como se muestra en la siguiente figura:
Más sobre la parábola
Una parábola general que se abre a lo largo del eje y, con el vértice en el origen \((0, 0)\) tiene la siguiente representación funcional \(y = 4ax^2\).
Entonces, por simetría, una parábola general que se abre a lo largo del eje x, con el vértice en el origen \((0, 0)\) tiene la siguiente representación funcional \(x = 4ay^2\).
Luego, se puede obtener un vértice general aplicando una traslación a un punto dado \((k, h)\).
Aplicaciones
La parábola tiene innumerables aplicaciones en Física, debido a la forma en que operan la fuerza de gravedad y las leyes de Newton, la trayectoria de la mayoría de los cuerpos que son arrojados seguirá una trayectoria parabólica.
Además, hablando algebraicamente, las parábolas aparecen en Álgebra todo el tiempo, porque todas las funciones cuadráticas tienen un gráfico parabólico, y las funciones cuadráticas aparecen MUCHO en Álgebra.
Además, las parábolas aparecen en Cálculo al encontrar mínimos y máximos. Resulta que muchos problemas de maximización y minimización tienen una función cuadrática para maximizar, y geométricamente, el máximo o mínimo (dependiendo de si la parábola se abre hacia arriba o hacia abajo) se logra en el vértice.
Otras secciones cónicas que puede interesarle conocer son las elipse , el hipérbola y el circulo .