La elipse
Una Elipse es el lugar geométrico de puntos en los ejes de coordenadas que tienen la propiedad de que la suma de las distancias de un punto dado de la elipse a dos puntos fijos (los focos) es igual a una constante, que denominamos \(2a\).
El concepto de "lugar geométrico" es muy atractivo desde un punto de vista conceptual, pero puede que no le dé una visión clara de lo que está tratando de representar.
Intente hacer el ejercicio de mirar la ecuación a continuación y vea si puede averiguar cómo se ve gráficamente;
¿Podrías averiguar cómo funciona la gráfica con solo mirar la ecuación anterior? Ya me lo imaginaba. Déjame presentarte la elipse:
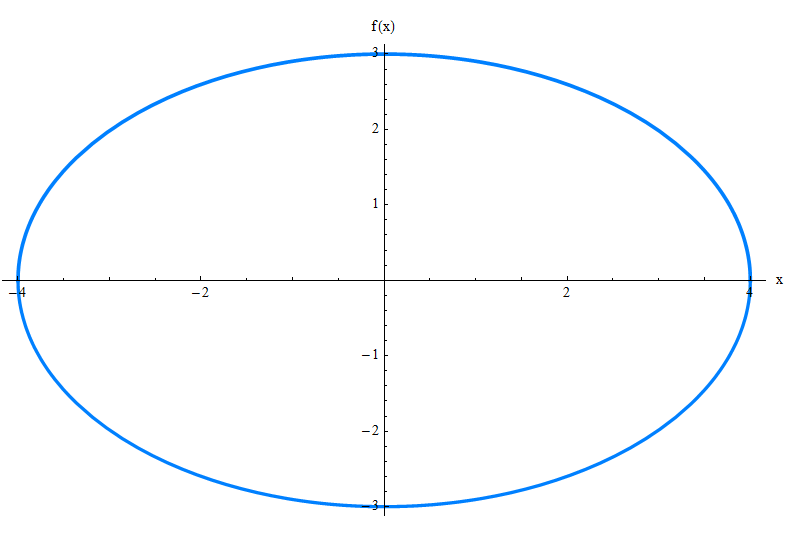
La ecuación general de la elipse
Sin mucha discusión teórica, estableceremos que la ecuación general de la elipse con centro en el origen y focos en el eje x, para \(a \ge b\) es
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Para la elipse descrita anteriormente, tiene focos en los puntos \((-c, 0)\) y \((c, 0)\), donde \(c = \sqrt{a^2 - b^2}\).
Ahora, ¿qué sucede con la ecuación de la hipérbola anterior cuando \(b > a\)?
En ese caso, los focos están en el eje y, y son \((0, -c)\) y \((0, c)\), donde \(c = \sqrt{b^2 - a^2}\).
Ahora bien, si quisiéramos desplazar el centro a un punto \((k,h)\)?
Todo lo que tiene que hacer en ese caso es reemplazar \(x\) por \(x-k\) y reemplazar \(y\) por \(x-h\).
Por lo tanto, al hacer una traslación, obtenemos que la ecuación de una elipse general es
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]La elipse de arriba tiene un centro en \((k,h)\) y tiene focos en \((k-c, h)\) y \((k+c, h)\) donde \(c = \sqrt{a^2 - b^2}\) para \(a \ge b\), y \((k, h-c)\) y \((k, h+c)\) donde \(c = \sqrt{b^2 - a^2}\) para \(b>a\).
EJEMPLO 1
Encuentra los focos de la elipse:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]RESPONDEDOR:
En primer lugar, según la estructura de la ecuación anterior, la elipse se centra en el origen \((0, 0)\). Observe que el semieje principal es 4, que está asociado con \(9y\), por lo que los focos están en el eje y.
De la ecuación obtuvimos que \(a^2 = 9\) y \(b^2 = 16\). Encontramos que \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Por lo tanto, los focos están en \((0, -\sqrt{7})\) y \((0, \sqrt{7})\).
EJEMPLO 2
Encuentre la ecuación de la elipse centrada en \((0, 2)\) con un foco en \((6, 2)\) y un eje semi-menor con un tamaño de 3.
RESPONDEDOR:
Según la información proporcionada, \(c = 6 - 0 = 6\). Dado que los focos están en una forma paralela al eje x, obtenemos que \(b = 3\) y luego \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)
Por tanto, la ecuación de la elipse es:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]La elipse y las secciones cónicas generales
Al igual que en el caso de la parábola, la hipérbola y el círculo, la elipse está estrechamente relacionada con el cono. El matemático griego antiguo llamado Apolonio descubrió esta conexión, con lo que se llama secciones cónicas .
Una sección cónica corresponde a las formas que se forman cuando se hace un corte a través de un cono con un plano, y según el ángulo relativo del cono y el plano, la forma de la sección transversal cambia.
De hecho, dependiendo del ángulo entre el cono y el plano, la forma de la sección transversal puede ser una parábola, un círculo, una elipse o una hipérbola. Esto se muestra en el siguiente gráfico:
Más sobre la elipse
Para una elipse con la ecuación \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \), con \(a \ge b\), \(a\) se llama semi-eje mayor y \(b\) se llama semi-eje menor.
Ahora, para \(b > a\), esa denominación se invierte, por lo que \(a\) se llamaría eje semieje menor y \(b\) se llamaría eje semieje mayor.
Excentricidad
La excentricidad de una elipse se calcula utilizando la siguiente fórmula:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]Este parámetro de excentricidad muestra indica cuánto se aparta la forma de la elipse de una versión simétrica de la elipse (que es el círculo, que tiene excentricidad \(e = 1\)).
Aplicaciones
La elipse tiene muchas aplicaciones. En ciencia, se usa ampliamente en Astronomía. De hecho, los planetas descritos órbitas elípticas alrededor del sol.
Algebraicamente, una elipse se parece mucho a una hipérbola, pero sus propiedades son radicalmente diferentes.
También te puede interesar conocer la parábola, para lo cual puedes consultar este tutorial . También puedes echar un vistazo a nuestro tutorial de hipérbola . Finalmente, también puede aprender todo lo que hay que hacer aprender sobre el círculo .