La hipérbola
Una hipérbola es el lugar geométrico de puntos en los ejes de coordenadas que tienen la propiedad de que la diferencia entre las distancias a dos puntos fijos (los focos), es igual a una constante, que denominamos \(2a\).
Naturalmente, eso suena un poco intimidante y demasiado técnico, pero de hecho es la forma en que se define una hipérbola.
Quizás, si te doy la ecuación de una hipérbola, la "reconocerías".
Probemos: esta es la ecuación de una hipérbola muy general:
¿Podrías averiguar cómo se ve con solo verificar su ecuación? Probablemente no. Así que presento la hipérbola, gráficamente para ti:
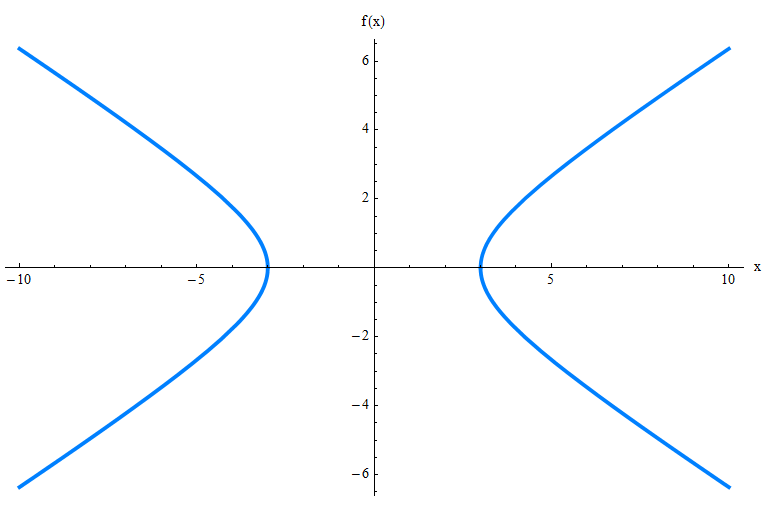
El gráfico anterior le muestra solo el gráfico de la hipérbola, pero hay muchos otros elementos que debe conocer, como las asíntotas oblicuas, los vértices y los focos. Consulte el gráfico a continuación.
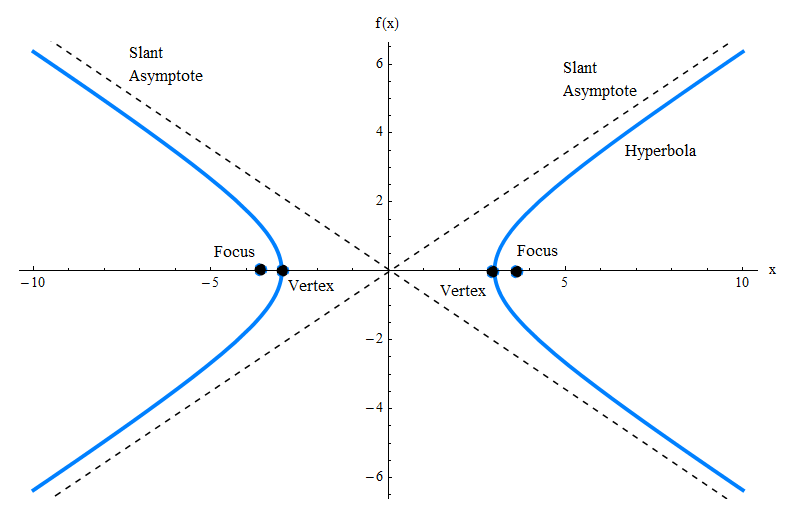
La ecuación general de la hipérbola
Sin mucha discusión teórica, diremos que la ecuación general de la hipérbola con focos en el eje x es
\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
Para la hipérbola descrita por la ecuación anterior, tiene vértices en los puntos \((-a, 0)\) y \((a, 0)\) y tiene focos en los puntos \((-c, 0)\) y \((c, 0)\), donde \(c = \sqrt{a^2 + b^2}\).
Una característica interesante de esta hipérbola es que tiene dos asíntotas inclinadas
Asíntota 1
: \(\displaystyle y = \frac{b}{a}x\)
Asíntota 2
: \(\displaystyle y = -\frac{b}{a}x\)
Ahora bien, ¿qué sucede con la ecuación de la hipérbola, si en cambio los vértices se trasladan por un punto dado \((k,h)\)?
Todo lo que tiene que hacer en ese caso es reemplazar \(x\) por \(x-k\) y reemplazar \(y\) por \(x-h\).
Por tanto, al hacer una traslación, obtenemos que la ecuación de una hipérbola general es
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]La hipérbola anterior tiene vértices en los puntos \((k-a, h)\) y \((k+a, h)\) y tiene focos en los puntos \((k-c, h)\) y \((k+c, h)\), donde \(c = \sqrt{a^2 + b^2}\).
Las ecuaciones de las asíntotas inclinadas son \(y = \frac{b}{a}(x-k) + h\) y \(y = -\frac{b}{a}(x-k) + h\).
¿Qué sucede con las hipérbolas que se abren a lo largo del eje y?
Por simetría, todo lo que tenemos que hacer es simplemente reemplazar los roles de \(x\) y \(y\) en la ecuación general de la hipérbola que ya tenemos. En la práctica, esto significa que dondequiera que aparezca \(x\) en la ecuación de la parábola que tenemos, lo cambiamos \(y\), y viceversa por \(y\).
Entonces, en el caso de una hipérbola que se abre a lo largo del eje x, la ecuación general es
\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]La hipérbola anterior tiene vértices en los puntos \((k, h - b)\) y \((k, h+b\) y tiene focos en los puntos \((k, h-c)\) y \((k, h+c)\), donde \(c = \sqrt{a^2 + b^2}\).
Las ecuaciones de las asíntotas inclinadas son \(y = \frac{b}{a}(x-k) + h\) y \(y = -\frac{b}{a}(x-k) + h\).
EJEMPLO 1
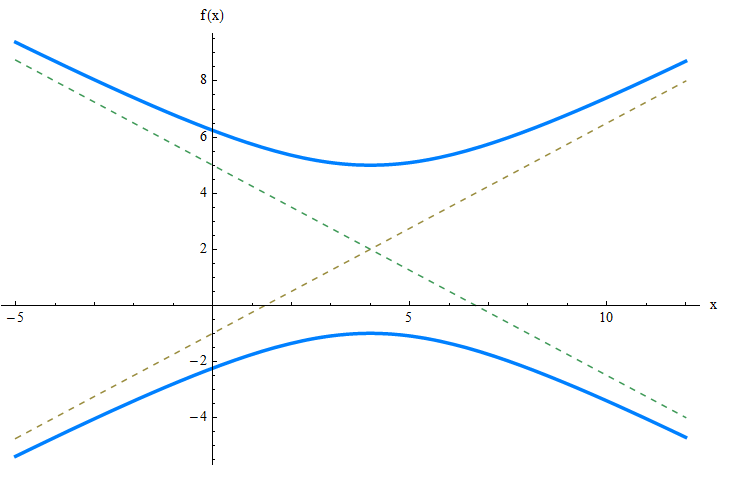
Encuentre los focos, vértices y asíntotas inclinadas de la hipérbola:
\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]RESPONDER:
Esta hipérbola se abre a lo largo del eje y. En este caso, los valores de traducción son \(k = 4\) y \(h = 2\). Además, obtenemos que \(a = \sqrt{16} = 4\) y \(b = \sqrt{9} = 3\). Por lo tanto, obtenemos que \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).
Por lo tanto, los focos son \((k, h-c) = (4, 2 - 5) = (4, -3)\) y \((k, h+c) = (4, 2 + 5) = (4, 7)\).
Los vértices son \((k, h-b) = (4, 2 - 3) = (4, -1)\) y \((k, h+b) = (4, 2 + 3) = (4, 5)\).
Las asíntotas oblicuas son
\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]Gráficamente:
EJEMPLO 2
Encuentre la ecuación de la hipérbola con focos en el vértice \((-4, 0)\) y \((4, 0)\), enfóquese en \((6, 0\).
RESPONDER:
Observe que los focos y los vértices están en el eje x, entonces la hipérbola se abre a lo largo del eje x. Además, dado que los focos son simétricos con respecto al origen, y un vértice es \((4, 0)\), obtenemos que \(a = 4\). Y dado que un foco está en \((6, 0)\), obtenemos ese \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).
Por tanto, la ecuación de la hipérbola es:
\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]La hipérbola y las secciones cónicas generales
Al igual que en el caso de la parábola, la hipérbola está estrechamente relacionada con el cono. De hecho, un matemático griego llamado Apolonio fue quien descubrió esta conexión, al comprender el concepto de secciones cónicas.
Una sección cónica ocurre cuando se hace un corte de un cono con un plano, y dependiendo del ángulo relativo del cono y del plano en el punto de corte, el cono se corta de una manera en la que la sección transversal tiene una forma específica. .
Entonces, dependiendo del ángulo relativo de corte, tenemos diferentes formas de la sección, y estas son la parábola, el círculo, elipse y la hipérbola. Vea el gráfico a continuación:
Más sobre la hipérbola
Una hipérbola con vértice en el origen, que se abre a lo largo del eje x tiene la ecuación \(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \), mientras que una hipérbola, que se abre a lo largo del eje y tiene la ecuación \(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1 \).
Entonces, se puede obtener un vértice general simplemente aplicando una traslación a un punto dado \((k, h)\).
Aplicaciones
La hipérbola tiene muchas aplicaciones en el mundo práctico, así como en Astronomía. Una diferencia con la parábola es que la hipérbola tiene asíntotas inclinadas, que la parábola no tiene.
Hablando algebraicamente, una hipérbola se parece mucho más a una elipse que a una parábola, aunque la diferencia de signo con la elipse hace un mundo de diferencia en su forma y propiedades.
Otro tipo importante de sección cónica es la parábola, de la cual puede aprender en este tutorial . Además, también puede aprender todo lo que hay que hacer aprender sobre el círculo y la elipse .