Aprender a factorizar es una de las habilidades más importantes que puede aprender. El factoraje tiene tantas aplicaciones, que estará encantado de tomarse el tiempo para aprender todo lo que hay al respecto.

Un repaso rápido sobre la propiedad conmutativa, asociativa y distributiva. Para los números reales \(x\), \(y\) y \(z\), tenemos las siguientes propiedades

(Asociatividad de la suma) \((x+y)+z = x+(y+z)\)

Conmutatividad de la suma) \( x + y = y + x\)

(Propiedad distributiva) \( x \cdot (y+z) = x \cdot y + x \cdot z\)

donde \(+\) y \(\cdot\) son la suma y el producto de números reales, respectivamente.

¿Por qué es útil saber factorizar?

Hay muchas razones, pero una de las cruciales es que la factorización nos brinda una manera fácil de resolver ecuaciones. De hecho, factorizar es LA forma en que tenemos que resolver ecuaciones.

Por ejemplo, considere la ecuación en la que estamos tratando de resolver para \(x\):

¿Cómo lo hacemos? Bueno, podemos usar la propiedad distributiva para obtener:

Por tanto, con esta última expresión \( x(y+z) = 0\) tenemos un ejemplo de factorización. De hecho, tomamos la expresión inicial, \(xy+xz\) y la factorizamos en \( x(y+z)\).

Entonces, ahora necesitamos resolver una ecuación más fácil, que es \( x(y+z) = 0\). ¿Por qué es más fácil? Es porque ahora que sabemos que el producto \( x(y+z)\) es igual a cero, entonces uno de los factores NECESITA ser igual a cero.

Entonces, si sabemos que \(y+z = \not 0\), entonces sabemos que necesitamos tener ese \(x = 0\).

LECCIÓN : Una ventaja de la factorización es poder escribir una ecuación como una multiplicación de factores que es igual a cero. Entonces, AL MENOS UNO DE LOS FACTORES DEBE SER CERO.

Por ejemplo, cuando necesitamos resolver para \(x\) en la siguiente ecuación:

no nos damos cuenta de que en realidad estamos factorizando cuando lo hacemos

así que hemos reducido nuestra ecuación a un producto de factores que es igual a cero: \(8x = 0\). Dado que uno de los factores \(8\) no es igual a cero, entonces la única solución posible es \(x = 0\).

En otras palabras : si sabe factorizar, probablemente sepa como resolver ecuaciones .

Cómo factorizar polinomios

El equilibrio se alcanza con una clase muy general de expresiones que, a menudo, podemos factorizar de manera muy sistemática. Esa clase es la clase de polinomios. Por ejemplo, la expresión

es un polinomio de grado 2. O la siguiente expresión

es un polinomio de grado 3.

En general, una expresión de la forma

es un polinomio de grado \(n\). Naturalmente, cuanto más simple sea la expresión, más fácil será simplificar, por lo que primero deberíamos intentar aprender a factorizar expresiones cuadráticas. Es decir, polinomios de grado dos.

EJEMPLO 1

Factoriza la siguiente expresión cuadrática

RESPONDER:

Este ejemplo le mostrará, a propósito, que puede ser complicado factorizar incluso la expresión más simple, como la anterior. ¿Qué harías para factorizarlo?

¿Qué pasa si te digo que debes agregar cero? Es algo ridículo, ¿verdad? Veamos:

¿Estás de acuerdo con lo anterior? Acabo de agregar \(0\). Nada ha cambiado. Pero, ¿y si te digo que \(0 = 2x - 2x\)? Por lo que entonces

¡Todos iguales! Funciona, porque agregué cero, así que nada cambia. Pero ahora lo expandimos y lo agrupamos:

Entonces, finalmente, \(x^2 + x - 2 = (x+2)(x-1)\). ¿Difícil? Quizás, pero esa es una forma de hacerlo. A pesar de ser una forma inteligente de hacerlo, preferiríamos una forma más sistemática.

Factorizar un polinomio cuadrático

Los trucos inteligentes están bien, y todo eso, pero por lo general preferiremos un enfoque sistemático, que nunca falla. Para polinomios cuadráticos (polinomios de grado 2), existe una forma sistemática de proceder con la factorización:

Paso 1 : Dada la expresión cuadrática \(ax^2 + bx + c\), primero resolvemos la ecuación

Paso 2 : Si las soluciones (raíces) de la ecuación anterior son reales (incluso si solo hay una raíz), llamamos a esas raíces \(x_1\) y \(x_2\). Con estas raíces, obtenemos los siguientes factores:

por lo que las soluciones \(x_1\) y \(x_2\) determinan completamente los factores.

Naturalmente, en este caso, como se esperaba, la resolución de una ecuación cuadrática está estrechamente relacionada con la factorización de la ecuación cuadrática.

EJEMPLO 2

Factoriza la siguiente ecuación cuadrática

calculando sus raíces.

RESPONDER:

Comenzamos resolviendo la ecuación cuadrática correspondiente:

usando el famoso y conocido Fórmula cuadrática :

lo que implica que las soluciones (raíces) son \(x_1 = 1\) y \(x_2 = 1\). Entonces, la expresión cuadrática \(x^2 - 4x + 3\) se puede factorizar de la siguiente manera:

Observe que en este caso el término que multiplica el término \(x^2\) es 1, entonces en este caso \(a = 1\).

Factorizar polinomios con grado superior a 2

Entonces, para factorizar polinomios cuadráticos, simplemente calculo las raíces de la ecuación cuadrática correspondiente. ¿Cómo factorizo ​​polinomios de grado superior? Usando exactamente el mismo método .

Paso 1: Dada la expresión polinomial \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\), primero resolvemos la ecuación

Paso 2: Si las soluciones (raíces) de la ecuación anterior son reales (incluso si se repiten), llamamos a esas raíces \(x_1\), \(x_2\), ..., \(x_n\). Con estas raíces, obtenemos los siguientes factores:

Entonces, parecería que es igualmente simple factorizar un polinomio de grado 2 que factorizar un polinomio de grado 10. Teóricamente, la respuesta es sí.

El único problema es que no existe una fórmula algebraica simple y cercana que pueda resolver raíces para una ecuación polinomial de grado 5 o superior.

A veces, podemos resolver ecuaciones de grado superior mirando el gráfico o incluso usando la calculadora. Por ejemplo, consulte el siguiente gráfico:

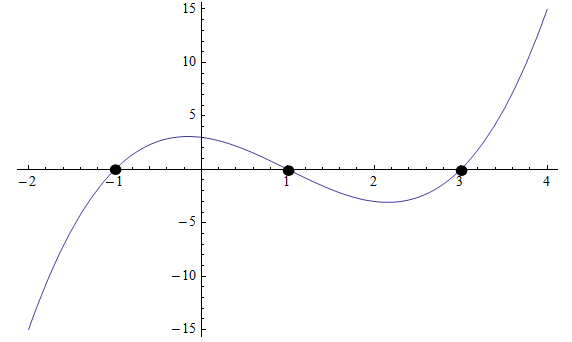
Gráficamente, podemos ver que el polinomio cruza el eje x en tres puntos: \(x_1 = -1\), \(x_2 = 1\) y \(x_3 = 3\), por lo que estas son las raíces.

Entonces, sabemos que el polinomio debe tener la forma \(p(x) = a(x+1)(x-1)(x-3)\). Necesitaríamos saber un punto más para conocer la constante \(a\).