Resolver ecuaciones logarítmicas
Resolver ecuaciones logarítmicas es algo que tendrá que hacer a menudo cuando trabaje con procedimientos algebraicos, y vale la pena desarrollar una estrategia concreta para lidiar con ellos.
Lo que aprenderá en este tutorial son las principales estrategias que debe seguir para resolver ecuaciones logarítmicas.
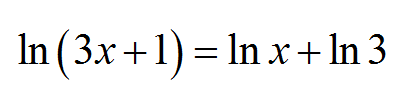
¿Qué es una ecuación logarítmica?
Lo primero que necesitamos es definir qué es una ecuación logarítmica.
Una ecuación logarítmica es una ecuación que involucra al menos una variable desconocida, donde aparece una expresión logarítmica en al menos un lado de la ecuación
.
Un ejemplo de una ecuación logarítmica es
\[\ln x = 2\ln x - \ln 3\]o tambien
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
Observe que una ecuación logarítmica puede contener más de una incógnita, como por ejemplo
Estrategias para resolver ecuaciones logarítmicas
El primer descargo de responsabilidad es que no hay formas a prueba de balas de resolver una ecuación logarítmica, ni una ecuación general para el caso. La razón de esto es que todos los métodos asumen una cierta estructura en la ecuación, que no está necesariamente en todas las ecuaciones.
Entonces, no podemos encontrar LA manera de resolver ecuaciones logarítmicas, porque no existe una manera única que trate con todos los casos posibles.
Aún así, hay un par de estrategias a seguir que le brindarán la mejor oportunidad de revisar la ecuación y encontrar una solución, si existe.
Primero, intente agrupar todas las expresiones logarítmicas en una expresión logarítmica.
Esto se logra normalmente mediante el uso de los reglas de registro , que le permiten compactar una expresión logarítmica, si la estructura de la expresión lo permite.
En segundo lugar, una vez que las expresiones logarítmicas se compactan tanto como sea posible, se deshará de ellas, normalmente aplicando la función exponencial a ambos lados de la igualdad.
Este último paso, con suerte, eliminará todos los logaritmos de la imagen y le permitirá resolver las incógnitas.
Entonces, en otras palabras, resolver una ecuación logarítmica consiste en agrupar las expresiones logarítmicas, eliminarlas aplicando exponencial y luego resolver la ecuación como una ecuación regular.
Obviamente, cuando te deshaces de los logaritmos, te enfrentas a una ecuación que podría tener sus propios desafíos.
Resolver diferentes ejemplos de ecuaciones logarítmicas
No hay mejor manera de aprender a resolver ecuaciones que practicar cómo resolverlas:
EJEMPLO 1:
Resuelve la siguiente ecuación:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]RESPONDER:
Sigamos las estrategias. La idea es compactar las expresiones logarítmicas tanto como sea posible. Esta es una decisión de criterio, porque la idea principal es esencialmente deshacerse de los logaritmos.
Usando las reglas de registro podemos poner el "4" dentro del logaritmo como
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Ahora que las expresiones logarítmicas están lo más compactadas posible, debemos deshacernos de los logaritmos.
Una forma de hacerlo es aplicar la función exponencial \(10^x\) a cada lado de la igualdad. ¿Qué quiero decir con eso ???
Bueno, tienes dos lados en esa igualdad. Dado que ambos lados son iguales, cuando se usan como argumentos de la función \(10^x\), debe preservar la igualdad. Entonces tenemos
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]porque sabemos que \(10^{\log a} = a\), que es una de las reglas básicas de registro.
Entonces, ahora que hemos eliminado los logaritmos, podemos resolver la ecuación que queda:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]entonces \(x_1 = 3 + 2\sqrt 2\) y \(x_2 = 3 - 2\sqrt 2\). Técnicamente, debe verificar si estas dos son soluciones de la ecuación original, para asegurarse de que pertenecen al dominio de las expresiones logarítmicas.
En este caso, tanto \(x_1 = 3 + 2\sqrt 2\) como \(x_2 = 3 - 2\sqrt 2\) son las soluciones de la ecuación original.
EJEMPLO 2:
Resuelve la siguiente ecuación logarítmica:
\[\large \ln 5 - \ln(6-x) = \ln x\]RESPONDER:
Usando las reglas de registro podemos compactar las expresiones de registro, obtenemos que
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]porque sabemos que \(e^{\ln a} = a\), que es una de las reglas básicas de registro.
Por tanto, ahora que hemos eliminado los logaritmos, podemos resolver la ecuación que nos queda:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]entonces \(x_1 = 1\) y \(x_2 = 5\). Inserte estos valores en la ecuación original para ver si de hecho son soluciones:
Para \(x_1 = 1\):
que es lo mismo que:
\[\large \ln 5 - \ln(5) = 0\]lo cual es cierto, entonces la ecuación se mantiene.
Para \(x_1 = 5\):
que es lo mismo que:
\[\large \ln 5 - \ln(1) = \ln(5)\]lo cual es cierto, entonces la ecuación se mantiene.
Por lo tanto, las soluciones de la ecuación son \(x_1 = 1\) y \(x_2 = 5\).
Más sobre la resolución de ecuaciones logarítmicas
Una cosa que más preocupa a los estudiantes es cómo deshacerse del log en una ecuación. Pero hemos visto que en realidad es la parte fácil. Lo que es más difícil es trabajar algebraicamente la expresión para que los registros puedan eliminarse.
Eso plantea la cuestión de cómo lidiar con diferentes bases, lo que requiere su propio párrafo.
Resolver ecuaciones logarítmicas con diferentes bases
En los ejemplos anteriores solo tratamos con \(\log\) (logaritmo con base 10) y \(\ln\) (logaritmo con base \(e\)). ¿Cómo lo haces cuando tienes un logaritmo con una base diferente, como \(\log_a\) ???
La respuesta es simple: para eliminar logaritmos con una base diferente, digamos \(\log_a\) que tiene la base \(a\), simplemente usamos la función exponencial \(a^x\). Simple ¿verdad?
De hecho, eliminar el logaritmo es la parte fácil de resolver ecuaciones logarítmicas. La parte más difícil del proceso es agrupar y compactar las expresiones logarítmicas en una forma que las elimine.
Puede obtener más información sobre cómo funciona la función logarítmica al ver las propiedades de su gráfica y estudiando el reglas básicas de registro .