Problema: Se ha proporcionado el siguiente resultado que resume los resultados de una logística regresión realizada en muestras pareadas de empresas que cotizan en bolsa del Reino Unido fallidas y no fallidas. Las variables independientes empleadas son las siguientes:

PBTCL_1 es la ganancia antes de impuestos dividida por el pasivo corriente.

CLTA_1 es el pasivo corriente a los activos totales.

NCI_1 es el intervalo sin crédito, que es una medida de cuánto tiempo (en días) una empresa puede seguir operando sin generar ingresos.

CATL_1 es el activo corriente al pasivo total.

Todos estos se calculan utilizando datos tomados de las últimas cuentas publicadas antes de la falla.

La variable dependiente es dicotómica, asignándose 1 a las empresas fallidas y 0 a las empresas que no lo están.

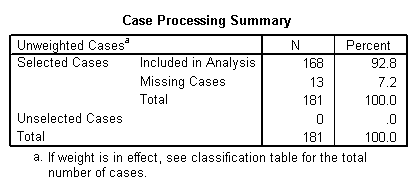
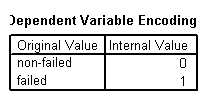
Bloque 0: Bloque inicial

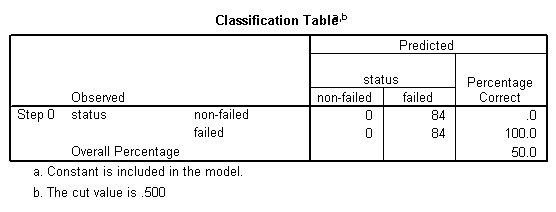
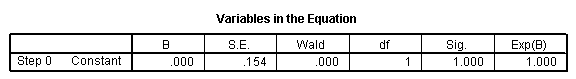
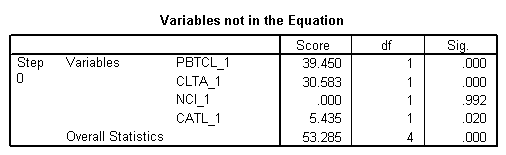
Bloque 1: Método = Entrar

Debe realizar una evaluación financiera y estadística de esta información.

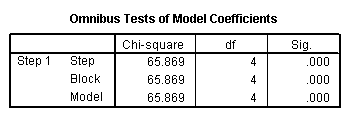
Solución: Observe que el modelo logístico es significativo en general, p = .000. Además, se encuentra que Nagelkerke R Cuadrado = .432, lo que indica una bondad de ajuste relativamente aceptable para este modelo.

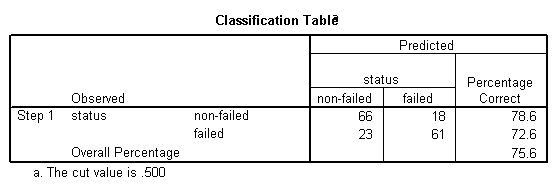
Se observa que entre las firmas que no quebraron, el 78.6% de ellas fueron correctamente clasificadas, mientras que entre las quebradas, el 72.6% de ellas fueron correctamente clasificadas, lo que representa un total del 75.6% de las firmas correctamente clasificadas en su conjunto , lo que indica una tasa de clasificación relativamente buena.

El modelo logístico es

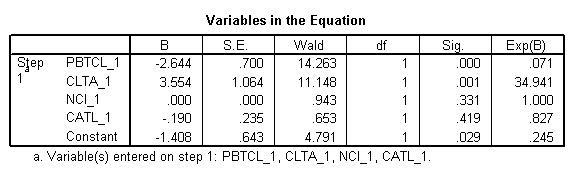
\[\ln \left( \frac{{\hat{p}}}{1-\hat{p}} \right)=-1.408-2.644*PBTCL\_1+3.554*CLTA\_1+0.000*NCI\_1-0.190*CATL\_1\]

donde \(\hat{p}\) corresponde a la probabilidad de que una empresa falle. Desde el punto de vista financiero, tenemos las siguientes conclusiones:

· Para un aumento de 1 punto en el beneficio antes de impuestos dividido por el pasivo corriente, las probabilidades de fracasar disminuyen en un 92,9%. Este cambio es significativo, p = 0.000 <0.05

· Para un aumento de 1 punto en el pasivo corriente al activo total, las probabilidades de fallar aumentan en 3294.10% Este cambio es significativo, p = 0.001 <0.05

· Para un aumento de un día en el intervalo sin crédito, las probabilidades de fallar no cambian. Este coeficiente no es significativo, p = 0.331> 0.05

· Para un aumento de 1 punto en el activo corriente al pasivo total, las probabilidades de fallar disminuyen en un 17.3% (esta disminución es significativa, p = 0.029 <0.05)