Cómo usar esta calculadora de prueba t para una muestra

Más información sobre el Prueba t para una media para que pueda interpretar mejor los resultados obtenidos por este salculadora: Una prueba t para una media es una prueba de hipótesis que intenta hacer una afirmación sobre la media de la población (\(\sigma\)). Esta prueba t, a diferencia de la prueba z, no necesita conocer la desviación estándar de la población \(\sigma\).

¿cómo realizar una prueba t para la media de una población?

La prueba tiene dos hipótesis complementarias, la hipótesis nula y la alternativa. La hipótesis nula es un enunciado sobre la media de la población, bajo el supuesto de que no tiene efecto, y la hipótesis alternativa es la hipótesis complementaria a la hipótesis nula. Las principales propiedades de una prueba t de una muestra para la media de una población son:

• Para una prueba t para una media, la distribución de muestreo utilizada para el estadístico de prueba t (que es la distribución del estadístico de prueba bajo el supuesto de que la hipótesis nula es verdadera) corresponde a la distribución t, con n-1 grados de libertad (en lugar de ser la distribución normal estándar, como en el caso de una prueba z para una media)


• Dependiendo de nuestro conocimiento sobre la situación "sin efecto", la prueba t puede ser de dos colas, de cola izquierda o de cola derecha.


• El principio fundamental de la prueba de hipótesis es que la hipótesis nula se rechaza si el estadístico de prueba obtenido es lo suficientemente improbable bajo el supuesto de que la hipótesis nula es verdadera.


• El valor p es la probabilidad de obtener resultados muestrales tan extremos o más extremos que los resultados muestrales obtenidos, bajo el supuesto de que la hipótesis nula es verdadera.


• En una prueba de hipótesis hay dos tipos de errores. El error tipo I ocurre cuando rechazamos una hipótesis nula verdadera y el error tipo II ocurre cuando no rechazamos una hipótesis nula falsa.

¿cómo calcular la estadística t para una muestra?

Entonces, ¿cuál es la fórmula de la prueba t de una muestra? En este caso, para esta fórmula de prueba t para el estadístico t es

\[t = \frac{\bar X - \mu_0}{s/\sqrt{n}}\]

La hipótesis nula se rechaza cuando el estadístico t se encuentra en la región de rechazo, que está determinada por el nivel de significancia (\(\alpha\)), el tipo de cola (bilateral, izquierda o derecha) y la número de grados de libertad \(df = n - 1\)

¿qué sucede con la prueba t cuando tengo 2 muestras?

Tenga en cuenta que esta es una calculadora de prueba t de una muestra. Si en cambio necesita comparar dos medias, debe usar un prueba t para muestras independientes , en cambio.

De manera similar, puede tener dos muestras pero están emparejadas, emparejadas o repetidas, en cuyo caso la herramienta adecuada a usar es esta calculadora de prueba t pareada , cuando ese es el caso.

Decisión para una prueba t de una muestra

¿Cómo se toma una decisión sobre una prueba t de una muestra? Primero, necesita conocer la estadística t, que llamamos \(t_{obs}\), y los grados de libertad df, para que pueda calcular el valor p.

El proceso de cálculo del p-valor dependerá del tipo de colas definidas. Para una prueba de dos colas, el valor p se calcula como \(p = \Pr(|t_{df}| > |t_{obs}|)\). Luego, para una prueba de cola izquierda, el valor p se calcula como \(p = \Pr(t_{df} < t_{obs})\), y para una prueba de cola derecha, el valor p se calcula como \(p = \Pr(t_{df} > t_{obs})\).

Ejemplo de prueba t de una muestra

Una vendedora tiene registros que muestran que el cliente promedio gasta $80 dólares en promedio en su tienda, pero recientemente siente que esa cantidad ha aumentado. Ella recolecta una muestra aleatoria de n = 30 clientes y encuentra que la cantidad media gastada en la tienda fue de $85.4, con una desviación estándar muestral de $12.4. ¿Tiene suficiente evidencia para afirmar que el gasto promedio en su tienda ha aumentado significativamente, en el nivel de significancia de 0,05?

Solución:

Se ha facilitado la siguiente información:

Hypothesized Population Mean \((\mu)\) =	\(80\)
Sample Standard Deviation \((s)\) =	\(12.4\)
Sample Size \((n)\) =	\(30\)
Sample Mean \((\bar X)\) =	\(85.4\)
Significance Level \((\alpha)\) =	\(0.05\)

(1) Hipótesis Nula y Alternativa

Se deben probar las siguientes hipótesis nula y alternativa:

\[ \begin{array}{ccl} H_0: \mu & = & 80 \\\\ \\\\ H_a: \mu & > & 80 \end{array}\]

Esto corresponde a una prueba de cola derecha, para la cual se utilizará una prueba t para una media, con desviación estándar poblacional desconocida, utilizando la desviación estándar de la muestra.

(2) Región De Rechazo

Según la información proporcionada, el nivel de significancia es \(\alpha = 0.05\) y el valor crítico para una prueba de cola derecha es \(t_c = 1.699\).

La región de rechazo para esta prueba de cola derecha es \(R = \{t: t > 1.699\}\)

(3) Estadísticas De Prueba

La estadística t se calcula de la siguiente manera:

\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar X - \mu_0}{s/\sqrt{n}} \\\\ \\\\ & = & \displaystyle \frac{ 85.4 - 80}{ 12.4/\sqrt{ 30}} \\\\ \\\\ & = & 2.385 \end{array}\]

(4) Decisión sobre la hipótesis nula

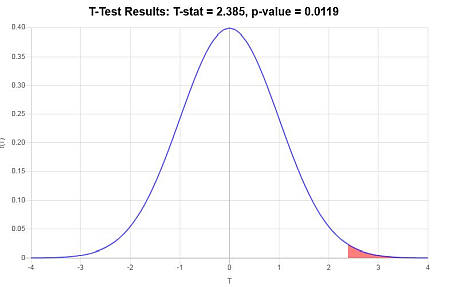
Dado que se observa que \(t = 2.385 > t_c = 1.699\), se concluye que se rechaza la hipótesis nula.

Usando el enfoque del valor P: El valor p es \(p = 0.0119\), y dado que \(p = 0.0119 < 0.05\), se concluye que se rechaza la hipótesis nula.

(5) Conclusión

Se concluye que la hipótesis nula Ho se rechaza. Por lo tanto, no hay evidencia suficiente para afirmar que la media poblacional \(\mu\) es mayor que 80, en el nivel de significancia \(\alpha = 0.05\).

Intervalo De Confianza

El intervalo de confianza del 95% es \(80.77 < \mu < 90.03\).

Gráficamente