Más sobre la matriz de correlación

Una matriz de correlación es una tabla en la que las correlaciones por pares entre varias variables se organizan convenientemente en forma de matriz. El valor de la i-ésima fila y la j-ésima columna corresponde a la correlación entre las variables \(X_i\) y \(X_j\).

En palabras simples, la matriz de correlaciones es un resumen de todas las correlaciones que se pueden encontrar para un conjunto de variables, para las cuales se dispone de datos de muestra.

El cálculo de la correlación es crucial, porque es el paso previo necesario para aplicar un Calculadora de regresión lineal para encontrar el modelo de mínimos cuadrados. Pero esto debe intentarse sólo cuando el se encuentra que la correlación es significativa .

Fórmula de matriz de correlación

Como \(corr(X_i, X_j) = corr(X_j, X_i)\), entonces la matriz de correlación es simétrica, y por ello, para no ser redundante, la matriz de correlación solo reporta los valores de la diagonal hacia arriba. Para otras operaciones de correlación, puede calcular un coeficiente de correlación mostrando todos los pasos, o puede usar este calculadora de correlación crítica .

¿cómo se calcula una matriz de correlación?

Para comprender cómo calcular una matriz de correlación, primero debe saber cómo calcular la correlación de Pearson, porque la matriz de correlación es simplemente la matriz de las correlaciones entre todos los posibles pares de variables.

Para continuar con el cálculo de la matriz de correlación, debe seguir estos pasos:

Paso 1: Enumere las variables que tiene, digamos X1, X2, ..., etc. Cada una de estas variables tiene una muestra asociada.

Paso 2: Tome las variables i-ésima y j-ésima de su lista, Xi y Xj, y calcule el coeficiente de correlación para ellas. Llámalo \(r_{ij}\)

Paso 3: Tome el valor \(r_{ij}\) y ese será el valor de la fila i, columna j de la matriz de correlación

Los valores de correlación cercanos a 1 o -1 indican fuertes asociaciones lineales, lo que sugiere que un Calculadora de regresión lineal (o un regresión lineal múltiple , dependiendo de cuántos predictores tenga).

¿cómo se utiliza una matriz de correlación?

Este es un punto que debe abordarse, ya que muchas veces una matriz de correlación puede presentarse en diferentes formatos. La matriz de correlación será una tabla con igual número de filas y columnas, donde aparecerá el nombre de las variables en las filas y columnas correspondientes.

Entonces, si la primera variable es \(X_1\), entonces la primera fila le dará el coeficiente de correlación de \(X_1\) y cada una de las otras variables. Y si la segunda variable es \(X_2\), entonces la segunda fila le dará el coeficiente de correlación de \(X_2\) y cada una de las otras variables, y así sucesivamente.

Según la forma en que se define esto, en la fila 1, columna 1 tienes la correlación de \(X_1\) consigo mismo, que es 1, luego en la fila 2, columna 2 tienes la correlación de \(X_2\) consigo mismo, que es también 1, y así sucesivamente.

Entonces, lo que sucede es que encontrará que la diagonal de la matriz de correlación siempre tiene solo unos. Dado que eso es algo que sucede siempre, muchas veces la matriz de correlación calculada omitirá la diagonal (porque ya sabemos que tiene unos, entonces, ¿cuál es el punto de escribirla explícitamente)?

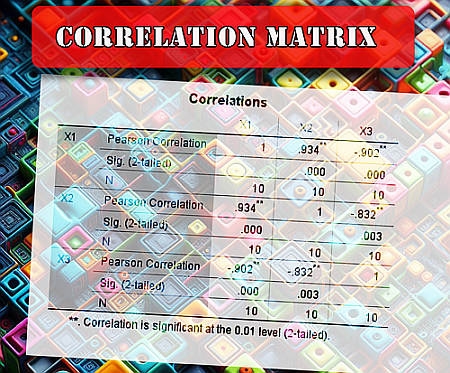
Pero hay otra cosa a observar: la correlación entre \(X_1\) y \(X_2\) es la misma que la correlación entre \(X_2\) y \(X_1\), por lo que la matriz de correlación es simétrico , entonces los valores debajo de la diagonal reflejan lo que tienes encima de la diagonal.

Es por eso que muy a menudo se ve una matriz de correlación con valores informados solo por encima (o por debajo) de la diagonal, porque sabemos que la diagonal es 1, y sabemos que los valores por debajo de la diagonal son un reflejo especular de los valores por encima de la diagonal.