Más información sobre esta calculadora de determinantes.

En el álgebra lineal y en el uso de las matrices, la idea del determinante de una matriz \(A\) es un concepto de la más profunda importancia.

Esto se debe a que su uso está ligado a casi todas las operaciones significativas que querrá hacer con las matrices, como la verificación de la invertibilidad de las matrices, encontrar la inversa de una matriz o sistemas de resolución .

Así que, mires donde mires cuando trabajes con matrices, encontrarás determinantes de una forma u otra. Por lo tanto, es muy importante familiarizarse con ellos.

¿Cómo puede ayudarle esta calculadora matricial?

1. Todo lo que tienes que hacer es escribir tu matriz
2. Tiene que ser una matriz cuadrada, es decir, una matriz con el mismo número de filas y columnas
3. Sólo tienes que pulsar el botón y la calculadora te mostrará todos los pasos y el valor final del determinante
4. Trabajar con cálculos de determinantes puede ser extremadamente laborioso y propenso a errores. Esta calculadora le evita esos problemas

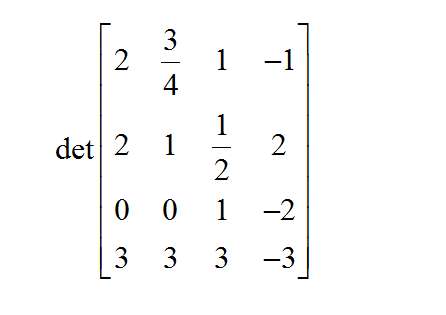
¿Cómo se calcula el determinante de una matriz?

La respuesta podría ser larga, porque hay muchas formas de calcular el determinante de una matriz. Digamos primero que los determinantes sólo se calculan para matrices cuadradas (es decir, matrices que tienen el mismo número de filas y columnas).

Así, la matriz más pequeña para la que podemos calcular un determinante es una matriz de 2x2. Consideremos una matriz genérica de 2x2, como se muestra a continuación:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

Cuál es la fórmula del determinante? En este caso, el determinante de la matriz \(A\) se calcula simplemente como \(\det(A) = a d - bc\)

Así, por ejemplo, si tuviéramos:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

el determinante de la matriz \(A\) sería \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\). Fácil, ¿verdad?

¿Cómo se encuentra el determinante de una matriz de 3x3?

Ahora, para matrices más grandes, construimos el cálculo del determinante basándonos en subdeterminantes de matrices más pequeñas. Para que te hagas una idea, veamos una forma de calcular el determinante de una matriz de 3x3. Consideremos

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

En este caso, el determinante de la matriz 3x3 \(A\) se calcula a partir de la operación de varios determinantes 2x2

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

En las ecuaciones anteriores los valores \(a\), \(b\), \(c\) desempeñan el papel de pivotes, y el pueden obtener un signo negativo. El signo de un pivote es \((-1)^{i+j}\), donde el pivote correspondiente está en la fila \(i\) y la columna \(j\).

Por ejemplo, \(a\) está en la fila 1, columna 1, por lo que su signo es \((-1)^{1+1} = (-1)^2 = 1\) (positivo). Además, \(b\) está en la fila 1, columna 2, por lo que su signo es \((-1)^{1+2} = (-1)^3 = -1\) (negativo), y así sucesivamente.

La magia consiste en elegir cualquier fila o columna como pivotes. Cada pivote tendrá asociado un signo (positivo o negativo) y un subdeterminante, que están relacionados con el cofactores de la matriz .

Este subdeterminante es el determinante real de la matriz original después de eliminar la fila \(i\) y la columna \(j\), para el pivote que está en la fila \(i\) y la columna \(j\).

La convención más lógica indica que se elija la fila o la columna con más ceros para los pivotes, a fin de evitar el cálculo de algunas de las subdeterminaciones, si es posible.

¿Cómo se encuentra el determinante de una matriz de 3x4?

No se puede hacer. Una matriz de 3x4 no es una matriz cuadrada y, por tanto, no se puede calcular ningún determinante. Para calcular un determinante, la matriz debe tener el mismo número de filas y columnas.

Una calculadora de determinantes 4x4

Para matrices más grandes, la metodología es la misma: elegir una fila o columna para los pivotes, idealmente la que tenga más ceros. A continuación, encuentre el signo correspondiente a cada pivote y encuentre los subdeterminantes correspondientes.

Así pues, se reduce el cálculo del determinante de una matriz 4x4 a la operación de cuatro determinantes 3x3. Y a su vez, cada uno de los determinantes de 3x3 se encuentra como la operación de varios determinantes de 2x2, para los que conocemos una fórmula.

Por lo tanto, puede ser un lío muy rápido.

Ejemplo de cálculo del determinante de una matriz

Pregunta: Considere la siguiente matriz:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Calcula el determinante de la matriz dada, mostrando los pasos.

Solución: Tenemos que calcular el determinante de la matriz \(3 \times 3\) que se ha proporcionado.

Utilizando la fórmula del subdeterminante obtenemos:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Conclusión : En base a los cálculos mostrados anteriormente, se encuentra que el determinante de la matriz es \(\det A = \displaystyle -15\).

Otras calculadoras matriciales útiles que puede utilizar

Los cálculos de matrices realizados a mano requieren mucho trabajo, por lo que puede aprovechar nuestros calculadoras de álgebra lineal.

En primer lugar, puedes utilizar esta calculadora de matrices inversas para calcular la inversa de una matriz mostrando los pasos, y puedes hacerlo método adjunto o utilizando Reducción de RREF .