Calculadora de Sistema de Ecuaciones a Forma Matricial
Instrucciones: Use esta calculadora para encontrar la representación matricial de un sistema dado de ecuaciones que proporcione. Especifique un sistema de ecuación lineal, ajustando primero la dimensión, si es necesario.
Luego, complete los coeficientes asociados a todas las variables y el tamaño de la mano derecha, para cada una de las ecuaciones. Si una variable no está presente en una ecuación específica, escriba "0" o déjelo vacío.
Más sobre esta Calculadora de Sistema de Ecuaciones a Forma Matricial
Una habilidad crucial cuando resolver sistemas de ecuaciones lineales es poder pasar del formato tradicional de sistemas lineales a matrices.
Una vez que tenga la representación matricial de un sistema lineal, puede aplicar regla de Cramer o puedes resolver el sistema primero encontrando el inverso de la correspondiente matriz de coeficientes.
O, con la representación matricial, puede construir la matriz aumentada y realizar el método de pivote de Gauss, lo que más le convenga.
Primero: ¿Cómo se escribe un sistema de ecuaciones en forma matricial?
Paso 1: Identifica cada una de las ecuaciones del sistema. Cada ecuación corresponderá a una fila en la representación matricial.
Paso 2: Ve trabajando en cada ecuación. Para cada uno de ellos, identifica el lado izquierdo y el lado derecho de la ecuación.
Paso 3: Lo que está en el lado izquierdo será parte de la matriz A, y lo que está en el lado derecho será parte del vector b
Paso 4: Los coeficientes de la izquierda deben identificarse por separado en términos de qué coeficiente multiplica cada variable.
Paso 5: Cada ecuación representa una fila y cada variable representa una columna de la matriz A.
¿Cómo se usa una matriz para resolver un sistema de ecuaciones?
Una vez que tiene un sistema en forma de matriz, hay una variedad de formas en que puede proceder para resolver el sistema. Por lo general, comienzas primero con calcular el determinante de la matriz , como criterio inicial para conocer las soluciones del sistema.
Cuando \(\det A \ne 0\), entonces sabemos que el sistema tiene una solución única. Ahora, cuando \(\det A = 0\), no significa que no tienes soluciones, solo significa que si hay soluciones, no es único.
De hecho, cuando \(\det A = 0\), no puedes usar Método de Cramer o el método inverso para resolver el sistema de ecuaciones . En ese caso, es mejor usar el método de pivote de Gauss.
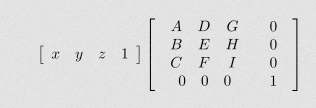
Cómo resolver ecuaciones matriciales
A menudo, se le proporciona un sistema de ecuaciones directamente en formato de matriz. Si ese es el caso, y el número de ecuaciones es el mismo que el número de variables, puede intentar usar el método inverso o la regla de Cramer. De lo contrario, puede utilizar el método de Gauss.
Ahora, puedes usar esta calculadora para expresar un sistema en una forma tradicional cuando se le da una forma matricial.



