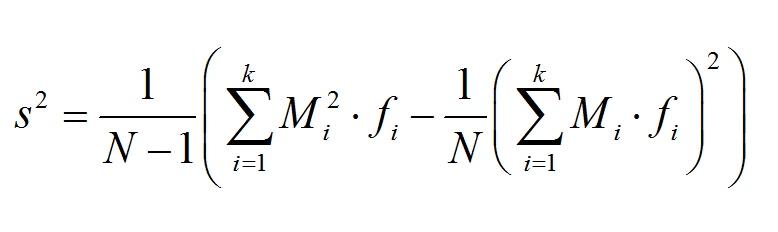Calculadora de análisis de varianza unidireccional

Más información sobre el Prueba ANOVA de una vía para que pueda comprender mejor los resultados entregados por este salculadora. En primer lugar, ANOVA o Análisis de Varianzas es uno de los campos más importantes de la Estadística. La razón de esto es que se centra en el análisis de la variación de las muestras exhibidas, al desglosar la variación total en varias fuentes de variación diferentes.

El uso más básico de ANOVA es probar la diferencia entre las poblaciones de varios grupos (2 o más). Recordemos que se usa una prueba t para comparar las medias de dos grupos, entonces ANOVA es una especie de extensión que permite realizar comparaciones para dos o más grupos.

Al igual que con cualquier otra prueba de hipótesis, ANOVA utiliza una hipótesis nula y alternativa. La hipótesis nula es un enunciado que afirma que todas las medias de la población son iguales, y la hipótesis alternativa es la hipótesis de que no todas las medias son iguales (observe que esto NO implica que todas las medias son desiguales, implica que al menos un par de medias es desigual).

¿cómo se calcula un anova?

Ejecutar una prueba ANOVA es un poco como ejecutar cualquier otra prueba paramétrica, y necesitará cumplir con algunas suposiciones. Los principales supuestos necesarios para realizar un ANOVA de una vía son:

• La variable dependiente (DV) debe medirse al menos en el nivel de intervalo


• Los grupos deben provenir de poblaciones normalmente distribuidas.


• Los grupos deben provenir de poblaciones normales con varianzas poblacionales iguales

Si los resultados del ANOVA son significativos, es decir, se rechaza la hipótesis nula, podemos realizar un Prueba post-hoc para evaluar exactamente qué pares difieren significativamente. Ejemplos de pruebas Post-Hoc son el LSD de Fisher, la prueba de Tukey, la corrección de Bonferroni, etc.

Las hipótesis nulas de una prueba ANOVA se rechazan cuando la Estadísticas F supera el valor de la relación F crítica que se calcula, en base a los grados de libertad correspondientes.

Cuando tiene k grupos y un tamaño de muestra total de N, entonces los grados de libertad del numerador son dfN = k - 1, y los grados de libertad del denominador son dfD = N - k - 2.

Cuando algunos de los supuestos no se cumplen (específicamente los segundos son terceros), existen opciones correctivas para algunas estadísticas más sólidas. Cuando existen violaciones graves a los supuestos, sería más apropiado utilizar una alternativa no paramétrica, como la prueba de Kruskal-Wallis.

Esta calculadora ANOVA con pasos le brinda suficiente información para rechazar o no rechazar la hipótesis nula, según la relación F calculada. Si se calcula la hipótesis nula, deberá realizar una prueba post-hoc.

Por qué no se usa una prueba t en su lugar

Dos pruebas T de muestras independientes están diseñadas para realizar comparaciones entre dos grupos. Cuando tiene más de dos grupos, la única forma de comparar es realizar varias comparaciones por pares.

Cada una de esas comparaciones por pares tiene una cierta probabilidad de un error de tipo I, por lo que el error de tipo I por familia es la probabilidad de que al menos una de esas comparaciones conduzca a un error de tipo I. Cuando se realizan muchas comparaciones, la probabilidad familiar de un error de tipo I se infla mucho.

Un ANOVA unidireccional está diseñado para comparar dos o más medias de muestra, pero si desea comparar dos medias de muestra, entonces puede ser más eficiente usar directamente nuestro prueba t para dos muestras independientes .

Alternativas no paramétricas a anova

ANOVA requiere que se cumplan ciertos supuestos, a saber, la normalidad y la homogeneidad de las varianzas. Se sabe que ANOVA es relativamente robusto a la violación de suposiciones, especialmente si son leves. Pero, ¿qué hacer cuando los supuestos simplemente no se cumplen?

En ese caso, puede utilizar nuestro Calculadora de la prueba de Kruskal-Wallis , que es el equivalente no paramétrico de ANOVA. Una ventaja de la prueba de Kruskal-Wallis es que puede usarla incluso con datos ordinales, para los cuales usar ANOVA no sería una buena idea.