Senkrecher -neigungsrechner
Anweisungen: Verwenden Sie dieses Grafikwerkzeug, um die Fundung der Neigung einer senkrechten Linie zu einer Linie mit einer bestimmten Steigung zu zeichnen.Bitte geben Sie die Steigung Ihrer Linie an (jeder gültige numerische Ausdruck).
Mehr zu diesem senkrechten neigungsrechner.
Oft müssen wir uns mit Linien und anderen Linien befassen, die ihnen senkrecht sind.Senkrechte hat mit einer 90 zu tun Ö Winkel zwischen den Linien.
Aber die Frage ist, wie wir das beziehen Senkrechte von Zwei Linien Mit den Hängen der beiden Zeilen?
Die Antwort ist einfach: zwei Zeilen mit Steigungen \(m_1\) und \(m_2\) sind senkrecht, wenn und nur wenn und nur wenn
\[m_1 \cdot m_2 = -1\]
Wie berechnet man die senkrechte steigung?
Die Antwort ist genau dort.Wenn Sie \(m_1\) wissen, müssen Sie nur die Steigung für die senkrechte Linie lösen, \(m_2\), damit wir die folgenden Formel für die Senkrechte Steigung :
\[\displaystyle m_2 = -\frac{1}{m_1}\]Welches ist die Formel für die senkrechte Neigung von der Hänge der Linie .
Wie berechnen sie die senkrechte steigung, wenn sie die gleichung einer linie haben?
In diesem Fall müssen Sie zuerst tun Konvertieren sie Die Gleisung in der Form des Steigungsschnittelns .Sobald Sie den Hang kennen, können Sie die oben dargestellte Formel verwenden.
Sobald Sie die Neigung der senkrechten Linie haben, können Sie letztendlich einen Punkt dieser senkrechten Linie durchlaufen Berechnen sie Die Gleisung der Senkrrecht Linie .
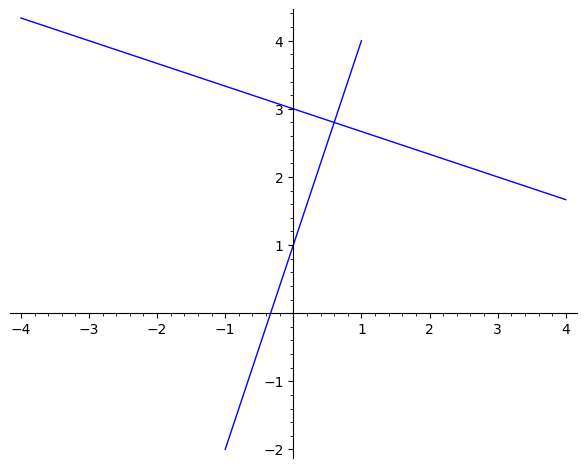
Beispiel: berechnung der steigung einer senkrechten linie
Betrachten Sie die Linie mit Gleichung \(x + 3y = 2)\).Finden Sie die Neigung der senkrechten Linie zur angegebenen Linie.
Lösung: Die Gleichung kann umgeschrieben werden wie: \[3y = -x + 2\] \[\Rightarrow y = \displaystyle -\frac{1}{3} x + \frac{2}{3}\] daher ist die angegebene Steigung der bereitgestellten Linie \(m = \displaystyle -\frac{ 1}{ 3}\) und wir müssen die senkrechte Steigung berechnen.
Die Formel, die zur Berechnung der senkrechten Steigung, \(m_{\perp}\) erforderlich ist, ist:
\[m_{\perp} = \displaystyle -\frac{1}{m}\]Indem wir den Wert von \(m = -\frac{ 1}{ 3}\) in der Formel anschließen, stellen wir fest, dass die senkrechte Steigung ist
\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{-\frac{ 1}{ 3}} = 3\]Daher schließen wir, dass die senkrechte Steigung \(m_{\perp} = 3 \) ist