Exponentenregeln
Die Operationen mit Exponenten gehören zu den häufigsten Operationen, die Sie in Mathe ausführen werden, und es ist entscheidend, dass Sie eine angemessene Grundlage dafür haben.
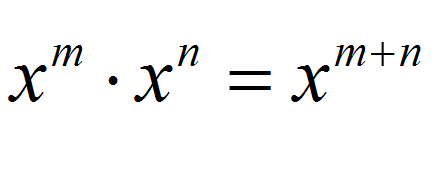
Lassen Sie uns ohne weiteres die grundlegenden Exponenteneigenschaften auflisten. Die effiziente Nutzung dieser Eigenschaften ist von größter Bedeutung. Die Regeln sind:
Regel 1: \(\large \displaystyle x^0 = 1\), für \(x = \not 0\)
Regel 2: \(\large\displaystyle x^1 = x\)
Regel 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regel 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regel 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Regel 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Lassen Sie uns diese Regeln ein wenig erklären in Worten .
Regel 1
sagt, dass alles, was auf die Potenz Null angehoben wird, gleich 1 ist. Nun, außer 0, weil gemäß Konvention (und es gibt einen guten Grund dafür) \(0^0 = 0\).
Jetzt,
Regel 2
sagt, dass das Nehmen einer beliebigen Zahl und das Erhöhen auf die Potenz von 1 dieselbe ursprüngliche Zahl ergibt. Mit anderen Worten, das Erhöhen einer Zahl auf die Potenz 1 hat keinen Einfluss auf die Zahl.
Regel 3
sagt, wenn ich Potenzen mit derselben Basis multipliziere, ist das Ergebnis eine Potenz mit derselben Basis, die zu einer Potenz erhoben wird, die der Summe der Exponenten der Potenzen entspricht, die ich multipliziere.
Regel 4
sagt, dass das Nehmen der Potenz einer Potenz dasselbe ist wie das Nehmen einer Potenz mit den multiplizierten Exponenten als Exponenten.
Regel 5
Wenn ich Potenzen mit derselben Basis teile, ist das Ergebnis eine Potenz mit derselben Basis, die zu einer Potenz erhoben wird, die der Subtraktion der Exponenten der Potenzen entspricht, die ich multipliziere.
Regel 6
sagt, wenn ich eine Potenz habe, die eine Multiplikation beeinflusst, dann ist das dasselbe wie das Multiplizieren jedes der Begriffe, die zu dieser Potenz erhoben werden.
BEISPIEL 1
Vereinfachen Sie den folgenden Ausdruck
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]ANTWORTEN:
Verwendung von Regel 5 für die Gewaltenteilung mit derselben Basis:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]Sollte ich mir Sorgen um negative Exponenten machen?
Nicht wirklich. Erstens geben die oben genannten 5 Regeln für Exponenten keine spezifische Aussage darüber ab, dass die Exponenten nicht negativ sein müssen. In der Tat funktionieren die Regeln alle gleich, die Exponenten sind negativ.
In der Tat für negative Exponenten Es gibt zwei Regeln, mit denen Sie sie in positive Exponenten umwandeln können:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
Dieser obige Ausdruck zeigt uns, dass wir eine Potenz mit einem negativen Exponenten im Zähler in eine Potenz im Nenner mit dem entsprechenden positiven Exponenten umwandeln können.
Dieser obige Ausdruck zeigt uns, dass wir eine Potenz mit einem negativen Exponenten im Nenner in eine Potenz im Zähler mit dem entsprechenden positiven Exponenten umwandeln können.
BEISPIEL 2
Vereinfachen Sie den folgenden Ausdruck und lassen Sie keine negativen Exponenten übrig:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]ANTWORTEN:
Die negativen Exponenten in positive Exponenten umwandeln und die 5 Exponentenregeln anwenden:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]Damit ist die Vereinfachung abgeschlossen.
Beziehen sich diese Exponentenregeln etwas auf die Regeln der Logarithmen?
Absolut! Probier das aus logarithmische Regeln und Sie werden feststellen, dass sie strukturell sehr ähnlich sind, und dies liegt daran, dass die Logarithmen und Potenzen inverse Operationen zueinander sind.
Lassen Sie uns als kleines Beispiel einen schnellen Beweis machen. Angenommen, \(a = x^m\) und \(b = x^n\). Dann per Definition \(m = \log_x a\) und \(n = \log_x b\). Also, nach den Exponentenregeln, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Daher per Definition \(m + n = \log_x (a \cdot b)\). Aber \(m = \log_x a\) und \(n = \log_x b\), also \(\log_x a + \log_x b = \log_x (a \cdot b)\).
Mehr über die Exponentenregel
Eine Sache, die wir hervorheben müssen, ist die Tatsache, dass die Regeln für Exponenten nicht erfordern, dass die Exponenten positiv sind. Die Exponenten müssen keine Ganzzahl sein. Die Regeln gelten für echte Exponenten.
• Vergessen Sie nicht, dass Sie einen negativen Exponenten im Zähler transformieren können, indem Sie ihn an den Nenner mit positivem Exponenten übergeben.
• Wenn Sie es mit einem negativen Exponenten im Nenner zu tun haben, können Sie ihn transformieren, indem Sie ihn an den Zähler mit positivem Exponenten übergeben.
Die Regeln der Exponenten haben so viele Anwendungen, einschließlich der Bereitstellung einer Basis für die Erlangung der Regeln zur Vereinfachung von Radikalen , die als Folge der Wurzeln von Exponenten kommen.
In grafischen Begriffen können Sie diese Regel anhand von untersuchen grafische Darstellung mögliche Exponentialfunktionen und sehen die spezifischen Eigenschaften, die sie haben.