Protokollregeln
Die logarithmische Funktion ist eine der wichtigsten Funktionen in der Mathematik. Die Protokollregeln sind einfach und bequem, sodass die Arbeit mit Logarithmen sehr einfach ist.
Erinnern wir uns zunächst an die Bedeutung von \(\log_b a\). In diesem Zusammenhang ist der Wert \(b\) der Base des Logarithmus und \(a\) ist der Streit .
Wir sagen, dass \(\log_b a = y\) wenn \(b^y = a\). Dies bedeutet, dass \(\log_b a\) die Zahl ist, auf die \(b\) (die Basis) angehoben werden muss, um \(a\) (das Argument) zu erhalten.
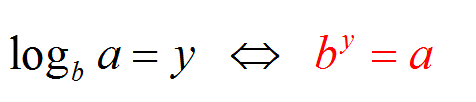
Zum Beispiel gehört \(\log_{10} 25\) der Zahl, auf die ich 10 gehört muss, um 25 zu erhalten. Der gesuchte Logarithmus ist auch die Zahl \(y\) mit der Einstellung \(10^y = 25\)
Die Frage ist nun, wie wir die Zahl \(y\) bezahlen, die sterben \(10^y = 25\) hat. Nun, diese Zahl ist gut zu verstehen und die logarithmische Funktion \(f(x) = \log_{10} x\) zu verlieren sich um. Diese Funktion ist keine Elementarfunktion und eine Taylor-Reihe.
Oder Sie können einen Taschenrechner gehört.
Die Log-Regeln: Eigenschaften von Logarithmen
Dies sind die wichtigsten Protokollregeln:
Regel 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Regel Nr. 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Regel Nr. 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Regel 4 : \(\large \log_a (a) = 1 \)
Regel Nr. 5 : \(\large \log_a (1) = 0 \)
BEISPIEL 1
Verein fordert Sie \(\log_2 8 + \log_2 4\) persönliche der Protokollregeln:
ANTWORTEN:
Unter Verwendung von Regel 1 stellen wir uns fest fest:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Der erste Schritt ist auch eine einfache Anwendung von Regel 1, aber wie bekommen wir das \(\log_2 32 = 5\)? Es liegt daran, dass \(2^5 = 32\), finden Sie auch in diesem Fall direkt, welche Zahl Sie zahlen, um \(2\) zu erhöhen, um \(32\) zu erhalten.
Für die größten Logarithmen müssen Sie einen Taschenrechner, um sie zu gehört. Es sind nur einige kurze, die Sie direkt gehört können. Sachen wie \(\log_{10} 100 = 2\), weil Sie leicht wissen, dass \(10^2 = 100\).
Aber können Sie \(\log_{10} 102\) direkt bezahlen? Nicht wirklich, gehört brauchst du einen Taschenrechner.
BEISPIEL 2
Unterschied Sie die Summe und Subtraktion der Logarithmen aus: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
ANTWORTEN:
Zuallererst müssen wir uns daran erinnern, dass das Ziehen einer Kubikwurzel das Erhöhen der \(\sqrt[3]{x}\)- Potenzhaften. Mit anderen Worten, \(\sqrt[3]{x}\) ist gehört wie \(x^{1/3}\).
Dann haben wir die Regel 3, um die Potenz für den Logarithmus zu bringen, und dann haben wir die Regeln 1 und 2 erhalten.
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]war notwendiger Krieg: Summe und Subtraktionen mussten Logarithmen.
Die Änderung der Basisformel für Logarithmen
Eine der wahrsten Formeln in Bezug auf Logarithmen ist die Arbeitsweise der Basisformel. Diese Formel lautet wie folgt:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Diese Formel bedeutet nur, dass, wenn Sie die Basis von \(b\) in \(c\) bestimmen, die Ergebnisse im Liegenen sind, Sie selbst durch den Logarithmus der neuen Basis dividieren müssen.
Wenn Sie nun künstlerisch orientiert sind, können Sie die alternative Form der Rechte der Rechte Formel werden, die unterlassen wird:
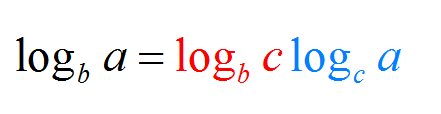
BEISPIEL 3
Unterscheiden Sie das persönliche Protokoll \(\ln\) in \(\log\) (Basis 10) aus.
ANTWORTEN:
Mit der Änderung der Basisformel erhalten wir beziehen:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Sie sagen auch, dass \(\ln a\) erhalten wird, entschädigt \(\log a\) durch \(\log e\) wird wird. Wie sicher? Wer sagt, dass Mathe schwer Krieg?
Mehr über die Log-Regeln
Logarithmen sind in der Mathematik sehr wichtig. Historisch gesehen spielen Logarithmen in der Astronomie eine sehr wichtige Rolle, um die Bewegung des Mondes und der Planeten vorhergehende.
Die logarithmischen Funktionen liegen in der Mitte von allem in Mathe, sie verflechten sich mit Exponential, Exponenten und so viel allem. Logarithmen auswendig zu lernen, weil sie wichtig sind.
Auch diese hier vor politischen Protokolle spielen eine Rolle Rolle bei der Steuerung des Auflösung logarithmischer Gleichungen .
Notationskonwirkungen
Es gibt einige Notationskonstellungen, die Sie kennen müssen. Im Allgemeinen schreiben wir \(\log_b a\) und sagen es "log base b of a". Wenn die Basis \(b = 10\) ist, schreiben Sie wir anspruchsell einfach \(\log a\). Wenn Sie auch ein \(\log\) ohne Basis sehen, wird, dass die Basis \(10\) ist.
Es gibt noch einen anderen anderen Wert fallen. Wenn für \(\log_b a\) die Basis \(b = e\) (die Eulerkonstante) ist, schreiben wir \(\ln a\) Aktivitäten von \(\log_e a\). Wenn auch \(\ln\) versucht von \(\log\) verwendet wird, liegt stirbt daran, dass die Basis des Logarithmus \(e\) ist.
Gehört Sie, dass \(\ln a\) sich auch darum kümmert wird erkennenliches Protokoll . Und ja, natürliche Protokolle haben Rechte wie das allgemeine Protokoll.
Wenn Sie eine logarithmische Funktion haben, die Sie grafisch darstellen können, können Sie unsere unsere Logarithmische Funktion Graph Maker , die Ihnen eine übersichtliche Grafik geben.
