Operationen mit negativen Exponenten
Die Operationen mit Exponenten gehören zu den grundlegendsten Operationen in der Algebra, und unter ihnen sind diejenigen, die negative Exponenten beinhalten, diejenigen, die den Schülern die meisten Komplikationen bringen.
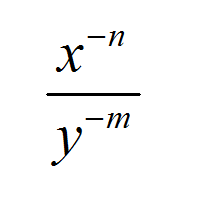
Erinnern wir uns zunächst an die grundlegenden Exponenteneigenschaften. Die Verwendung dieser Eigenschaften ist in den meisten Bereichen der Mathematik allgegenwärtig. Die Regeln sind:
Regel 1: \(\large \displaystyle x^0 = 1\), für \(x = \not 0\)
Regel 2: \(\large\displaystyle x^1 = x\)
Regel 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regel 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regel 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Wenn Sie beispielsweise einen Ausdruck wie \(3^5 \cdot 3^7\) haben, wissen wir, dass wir die Multiplikationsregel (Regel 3) verwenden, um Folgendes zu erhalten:
\[\large 3^5 \cdot 3^7 = 3^{5+7} = 3^{12}\]Die Exponentenregeln: Was passiert mit den negativen Exponenten?
Selbst wenn Sie es nicht erkannt haben, sagen die obigen Regeln nicht, dass die Exponenten positiv sein müssen. In der Tat könnten sie negativ sein und die Regeln werden auch gelten.
Aus den Regeln 1 und 5 können wir nun die Beziehung zwischen positiven und negativen Exponenten ableiten. Nehmen Sie für Regel 5 an, dass \(m = 0\) und \(n\) positiv sind. Dann bekommen wir
\[\large\displaystyle \frac{1}{x^n} = \frac{x^0}{x^n} = x^{0-n} = x^{-n}\]Der obige Ausdruck gibt uns eine einfache Beziehung zwischen positiven und negativen Exponenten:
\[\large\displaystyle \boxed{\frac{1}{x^n} = x^{-n}}\]
Dieser obige Ausdruck sagt uns, dass wir eine Potenz mit einem negativen Exponenten im Zähler an den Nenner mit dem entsprechenden positiven Exponenten übergeben können. Dies ist eine 'Regel' für negative Exponenten
Das Schöne an der obigen Formel ist, dass wir die Begriffe auf beiden Seiten der Gleichheit multiplizieren und den obigen Ausdruck in einer etwas anderen Form schreiben können:
\[\large\displaystyle \boxed{\frac{1}{x^{-n}} = x^{n}}\]
Dieser letzte Ausdruck ist normalerweise sehr nützlich, weil er uns sagt, dass wir eine Potenz mit negativem Exponenten im Nenner zum Zähler bringen können, aber mit dem entsprechenden positiven Exponenten. Dies kann als eine weitere "Regel" für negative Exponenten angesehen werden.
BEISPIEL 1
Vereinfachen Sie den folgenden Ausdruck und lassen Sie ihn ohne negative Exponenten:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2}\]ANTWORTEN:
Nach der Regel der negativen Exponenten schalten wir positive / negative Exponenten zwischen Zähler / Nenner um:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2} = \frac{x^{3}\sqrt{x} x^{1/2}}{ y^2 y^{3}}\] \[\large = \frac{x^{3} x^{1/2} x^{1/2}}{ y^2 y^3} = \frac{x^{3+1/2+1/2}}{ y^{2+3}} \] \[\large = \frac{x^{4}}{ y^{5}} \]und wir beenden die Vereinfachung, weil es nichts mehr zu vereinfachen gibt.
Mehr über negative Exponenten
Eine der größten Erkenntnisse aus diesem Tutorial über negative Exponenten ist, dass wir Regeln haben, um diese negativen Exponenten in positive Exponenten umzuwandeln. Wie machen wir das?
• Wenn der Zähler einen negativen Exponenten enthält (Sie multiplizieren also mit einem negativen Exponenten), können Sie ihn mit einem positiven Exponenten an den Nenner übergeben.
• Wenn der Nenner einen negativen Exponenten hat (Sie teilen also durch einen negativen Exponenten), können wir ihn mit positivem Exponenten an den Zähler übergeben.
Das Arbeiten mit negativen Exponenten ist nur ein kleiner Teil des Themas Regeln der Exponenten , die Ihnen einen klaren Einblick geben, warum der Fall mit negativen Exponenten so funktioniert, wie er funktioniert.