Die Parabel
Eine Parabel ist die geometrische Stelle von Punkten in den Koordinatenachsen, die die Eigenschaft haben, dass sie von einem festen Punkt (als Fokus bezeichnet) und einer Linie (als Directrix bezeichnet) gleich weit entfernt sind.
Ich weiß, was ein bisschen zu technisch klingt, aber wir werden es durchgehen, und am Ende werden Sie sehen, dass es nicht so schwer ist.
Würde es helfen, wenn ich das sagen würde?
die Funktion \(f(x) = x^2\) unterscheidet eine Parabel?
Sicher wird es helfen. Und Sie denken vielleicht: "Warum haben Sie mir nicht von Anfang an gesagt, dass die Parabel diese Funktion ist?".
Da es keine A-Parabel gibt, gibt es unendlich viele davon. Und eine Parabel muss nicht einmal durch eine Funktion dargestellt werden. Ja, einige Beziehungen sind Parabeln, wie wir sehen werden.
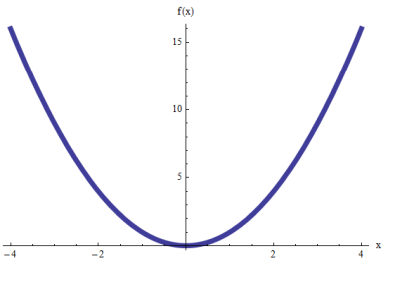
Eines ist wichtig zu erwähnen: Unter Verwendung von Funktionen und Beziehungen gibt es die Parabeln, die sich entlang der \(y\)- Achse "öffnen", und es gibt die Parabeln, die sich entlang der \(x\)- Achse "öffnen".
Am Ende ist es durch Symmetrie leicht zu erkennen, dass die Parabeln, die sich entlang der y-Achse "öffnen", dieselbe Struktur haben wie diejenigen, die sich entlang der x-Achse "öffnen". Es reicht also aus, zu lernen, wie man es macht Behandle einen Typ.
Die allgemeine Gleichung der Parabel
Es gibt einfache Ableitungen, um die Gleichung einer Parabel basierend auf der Position einer Directrix und dem Fokus zu erhalten, aber wir werden die Ableitung in dieser Einführung überspringen.
Überprüfen Sie die Grafik unten. Wir müssen einige entscheidende Elemente der Parabel identifizieren: Wir haben den Scheitelpunkt, den Fokus und den Directrix.
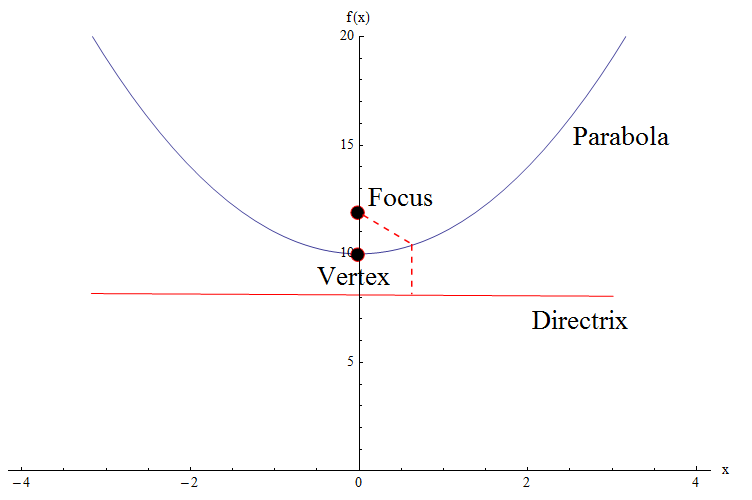
Wir werden nicht viel ins Detail gehen, aber wir werden sagen, dass die Gleichung einer allgemeinen Parabel mit einem Scheitelpunkt am Ursprung, wobei der Fokus \((0, a)\) und die Directrix gleich \(y = -a\) sind, lautet
Diese Parabel ist die Art von Parabel, die sich entlang der y-Achse öffnet.
Was passiert nun, wenn wir anstelle des Scheitelpunkts am Ursprung den Scheitelpunkt an einem bestimmten Punkt \((k,h)\) haben möchten?
Nun, das ist die Magie der Arbeit mit einem Koordinatensystem und alles, was wir brauchen, um eine Übersetzung nach dem Punkt \((k,h)\) durchzuführen? Aber wie macht man eine Übersetzung von \((k,h)\)?
Einfach! Wo immer Sie \(x\) haben, ersetzen Sie es durch \(x-k\), und wo immer Sie \(y\) haben, ersetzen Sie es durch \(x-h\).
Bei einer Übersetzung lautet daher die Gleichung einer allgemeinen Parabel mit einem Scheitelpunkt am Punkt \((k,h)\), wobei der Fokus \((k, h+a)\) und die Directrix gleich \(y = h-a\) sind
\[\large y-h = 4a(x-k)^2\]was geschrieben werden kann als
\[\large \boxed{ y = 4a(x-k)^2 + h }\]Was passiert mit den Parabeln, die sich entlang der x-Achse öffnen?
Durch Symmetrie wird dies einfach durch Ersetzen der Rollen von \(x\) und \(y\) in der Gleichung der Parabel erhalten, die wir bereits haben. In der Praxis bedeutet dies, dass überall dort, wo \(x\) in der Parabelgleichung vorkommt, \(y\) geändert wird und umgekehrt für \(y\).
Daher lautet die Gleichung einer allgemeinen Parabel mit Scheitelpunkt am Punkt \((h,k)\), wobei der Fokus \((h+a, k)\) und die Directrix gleich \(x = h-a\) sind:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Beachten Sie den Unterschied:
Wenn eine Parabel eine Directrix der Form \(y = -a\) hat, öffnet sich die Parabel entlang der y-Achse (nach oben oder unten, je nachdem, ob der Fokus über oder unter der Directrix liegt).
Wenn eine Parabel eine Directrix der Form \(x = -a\) hat, öffnet sich die Parabel entlang der x-Achse (links oder rechts, je nachdem, ob der Fokus links oder rechts von der Directrix liegt).
BEISPIEL 1
Finden Sie die Gleichung der Parabel, die eine Directrix \(y = -4\) und einen Fokus \((0, 4)\) hat. Finden Sie auch den Scheitelpunkt.
ANTWORTEN:
Der Scheitelpunkt befindet sich auf der Parabel, ist also von der Geraden \(y = -4\) und dem Fokus \((0, 4)\) gleich weit entfernt, sodass der Scheitelpunkt \(0, 0)\) ist. Andererseits lautet für eine Parabel mit Scheitelpunkt am Ursprung die Gleichung der Directrix \(y = -a\), also in diesem Fall \(a = 4\). Folglich ist die Gleichung der Parabel
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Grafisch:
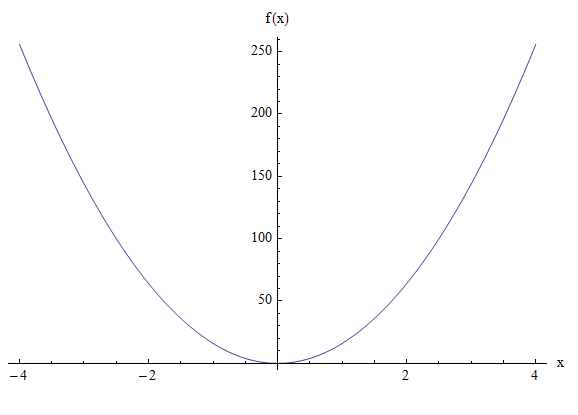
BEISPIEL 2
Finden Sie den Scheitelpunkt, den Fokus und die Richtung der Parabel \(y = 8x^2 - 16x + 9\).
ANTWORTEN:
Zunächst müssen wir das Quadrat vervollständigen:
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]Wenn wir dies mit der allgemeinen Gleichung gleichsetzen, stellen wir fest, dass sich der Scheitelpunkt am Punkt \((1, 1)\) befindet, und wir haben auch diesen \(4a = 8\), also \(a = 2\), daher ist die Directrix \(y = h - a = 1 - 2 = -1\) und der Fokus ist \((k, h + a) = (1, 1+2) = (1, 3)\).
Grafisch:
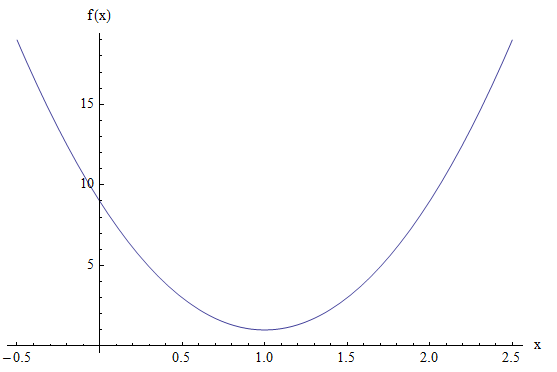
Die Parabel und allgemeine Kegelschnitte
So seltsam es auch sein mag, die Parabel ist eng mit dem Kegel verbunden. Wie würdest du sagen? Einem griechischen Mathematiker namens Apollonius wird zugeschrieben, mit der modernen Version der Kegelschnitte unter Verwendung von Koordinatensystemen beigetragen zu haben.
Apollonius und andere Mathematiker stellten fest, dass beim Schneiden eines Kegels mit einer Ebene der Kegel in Abhängigkeit vom relativen Winkel des Kegels und der Ebene so geschnitten wird, dass der Abschnitt unterschiedliche Formen aufweist.
Die verschiedenen Formen der Abschnitte, abhängig vom relativen Schnittwinkel, werden als Parabel, Kreis, Ellipse und Hyperbel bezeichnet, wie in der folgenden Abbildung dargestellt:
Mehr über die Parabel
Eine allgemeine Parabel, die sich entlang der y-Achse mit dem Scheitelpunkt am Ursprung \((0, 0)\) öffnet, hat die folgende funktionale Darstellung \(y = 4ax^2\).
Aus Symmetriegründen hat eine allgemeine Parabel, die sich entlang der x-Achse mit dem Scheitelpunkt am Ursprung \((0, 0)\) öffnet, die folgende funktionale Darstellung \(x = 4ay^2\).
Dann kann ein allgemeiner Scheitelpunkt erhalten werden, indem eine Übersetzung auf einen gegebenen Punkt \((k, h)\) angewendet wird.
Anwendungen
Die Parabel hat unzählige Anwendungen in der Physik. Aufgrund der Funktionsweise der Schwerkraft und der Newtonschen Gesetze folgt die Flugbahn der meisten herausgeworfenen Körper einer parabolischen Flugbahn.
Algebraisch gesehen erscheinen Parabeln die ganze Zeit in der Algebra, da alle quadratischen Funktionen einen parabolischen Graphen haben und quadratische Funktionen in der Algebra VIEL erscheinen.
Außerdem erscheinen im Kalkül Parabeln, wenn Minima und Maxima gefunden werden. Es stellt sich heraus, dass viele Maximierungs- und Minimierungsprobleme eine quadratische Funktion zum Maximieren haben und geometrisch das Maximum oder Minimum (abhängig davon, ob sich die Parabel nach oben oder unten öffnet) am Scheitelpunkt erreicht wird.
Andere konische Abschnitte, die Sie interessieren könnten, sind die Ellipse , das Hyperbel und das Kreis .