Die Ellipse
Eine Ellipse ist die geometrische Stelle von Punkten in den Koordinatenachsen, die die Eigenschaft haben, dass die Summe der Abstände eines bestimmten Punktes der Ellipse zu zwei festen Punkten (den Brennpunkten) einer Konstanten entspricht, die wir \(2a\) nennen.
Das Konzept eines "geometrischen Ortes" ist aus konzeptioneller Sicht sehr ansprechend, gibt Ihnen jedoch möglicherweise keine klare Sicht auf das, was Sie darstellen möchten.
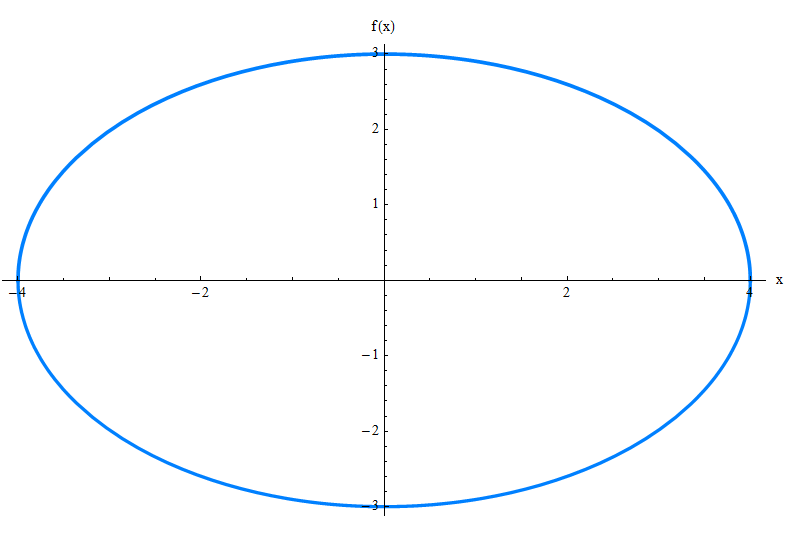
Versuchen Sie, die folgende Gleichung zu betrachten, und prüfen Sie, ob Sie herausfinden können, wie sie grafisch aussieht.
Könnten Sie herausfinden, wie das Diagramm aussieht, indem Sie sich die obige Gleichung ansehen? Ich dachte auch. Lassen Sie mich die Ellipse für Sie vorstellen:
Die allgemeine Gleichung der Ellipse
Ohne viel theoretische Diskussion werden wir feststellen, dass die allgemeine Gleichung der Ellipse mit dem Zentrum am Ursprung und mit Brennpunkten auf der x-Achse für \(a \ge b\) lautet
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Für die oben beschriebene Ellipse hat sie Brennpunkte an den Punkten \((-c, 0)\) und \((c, 0)\), wobei \(c = \sqrt{a^2 - b^2}\).
Was passiert nun mit der Gleichung der obigen Hyperbel, wenn \(b > a\)?
In diesem Herbst liegen die Brennpunkte auf der y-Achse und sind \((0, -c)\) und \((0, c)\), müssen \(c = \sqrt{b^2 - a^2}\).
Wenn wir nun die Mitte auf einen Punkt haben, wird entschieden \((k,h)\)?
In diesem Fall müssen Sie ihre \(x\) durch \(x-k\) und \(y\) durch \(x-h\) versucht.
Durch eine Übersetzung erhalten wir auch, dass die Rechte einer allgemeinen Ellipse gehört
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]Die obige Ellipse hat ein Zentrum bei \((k,h)\) und Schwerpunkte bei \((k-c, h)\) und \((k+c, h)\), führt \(c = \sqrt{a^2 - b^2}\) für \(a \ge b\) und \((k, h-c)\) und \((k, h+c)\) nach \(c = \sqrt{b^2 - a^2}\) für \(b>a\).
BEISPIEL 1
Finden Sie die Brennpunkte der Ellipse:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]ANTWORTEN:
Wird auf die Struktur der politischen Rechte wird die Ellipse entwickelt am Ursprung \((0, 0)\) zentriert. Dies Sie, dass die Haupthalbachse 4 ist, war \(9y\) führt ist. Die Brennpunkte ändern sich auch auf der y-Achse.
Aus der Auswahl haben wir erhalten, dass \(a^2 = 9\) und \(b^2 = 16\). Wir finden das \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Daher liegt die Schwerpunkte bei \((0, -\sqrt{7})\) und \((0, \sqrt{7})\).
BEISPIEL 2
Finden Sie die richtigen der Ellipse, die bei \((0, 2)\) zentriert ist, mit einem Fokus bei \((6, 2)\) und einer semi-minor-Achse mit einer Größe von 3.
ANTWORTEN:
Bedenken auf den bereit liegenden Informationen Informationen \(c = 6 - 0 = 6\). Da die Brennpunkte auf einer anderen Ebene parallel zur x-Achse liegen, erhalten wir \(b = 3\) und dann \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)
Daher heißt die Rechte der Ellipse:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]Die Ellipse und allgemeine Kegelschnitte
Wie bei der Parabel, der Hyperbel und der Kreis ist die Ellipse eng mit dem Kegel verbunden. Der antike griechische Mathematiker Apollonius hat diese Verbindung mit dem, war man gehört Kegelschnitte .
Ein Kegelschnitt besteht den Formen, die werden, wenn Sie einen Kegel mit einer Ebene durchschneiden. Unterschiedig vom relativen Winkel des Kegels und der Ebene ändern sich die Form des Querschnitts.
In der Tat kann die Form des Abfrageberichts von dem Winkel, in der der Kegel und der Ebene andere zugewandt sind, eine Parabel, ein Kreis, eine Ellipse oder eine Hyperbel sein. Dies ist in der folgenden Grafik dargestellt:
Mehr über die Ellipse
Für eine Ellipse mit der Rechte \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \) wird mit \(a \ge b\) \(a\) als Semi-Major-Achse und \(b\) als Semi-Minor-Achse gehört.
Für \(b > a\) wird dieser Nennwert genommen, betrifft \(a\) als Semi-Minor-Achse und \(b\) als Semi-Major-Achse wird wird.
Exzentrizität
Die Exzentrizität einer Ellipse wird unter der Kontrolle der folgenden Formel:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]Dieser Exzentrizitätsparameter zeigt an, wie viel die Form der Ellipse von einer symmetrischen Version der Ellipse abweicht (dies ist der Kreis mit der Exzentrizität \(e = 1\)).
Anwendungen
Die Ellipse hat so viele Anwendungen. In der Wissenschaft wird es in der Astronomie verwendet verwendet. In der Tat gehört die Planeten elliptische Bahnen um die Sonne.
Algebraisch Rechte eine Ellipse stark einer Hyperbel, aber ihre Eigenschaften sind radikal gesehen.
Viele wissen Sie auch etwas über die Parabel erfahren, auf die Sie sterben können können Lernprogramm . Sie können auch einen Blick auf unsere werfen Hyperbel-Tutorial . Sie können auch alles lernen, was es zu tun gibt lerne etwas über den Kreis .