Die Hyperbel
Eine Hyperbel ist die geometrische Stelle von Punkten in den Koordinatenachsen, die die Eigenschaft haben, dass die Differenz zwischen den Abständen zu zwei festen Punkten (den Brennpunkten) gleich einer Konstanten ist, die wir \(2a\) nennen.
Das klingt natürlich ein bisschen einschüchternd und zu technisch, aber es ist in der Tat die Art und Weise, wie eine Hyperbel definiert wird.
Wenn ich Ihnen die Gleichung einer Hyperbel geben würde, würden Sie sie vielleicht "erkennen".
Versuchen wir: Dies ist die Gleichung einer sehr allgemeinen Hyperbel:
Könnten Sie herausfinden, wie es aussieht, indem Sie nur die Gleichung überprüfen? Wahrscheinlich nicht. Also stelle ich die Hyperbel grafisch für Sie vor:
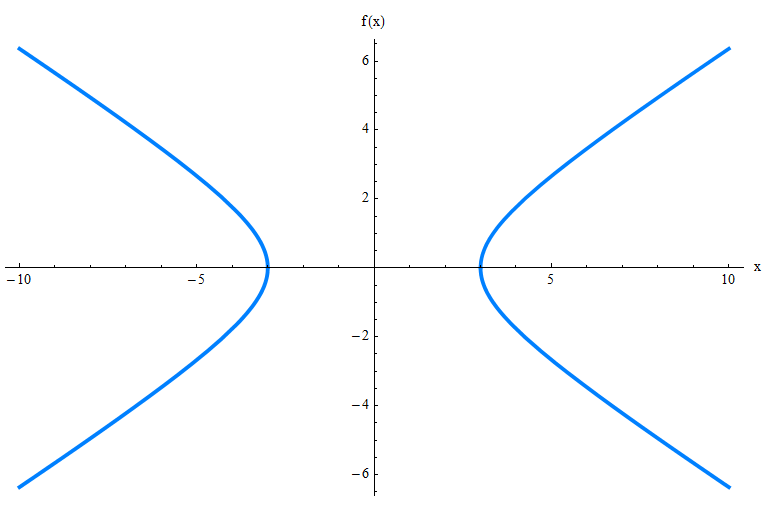
Das obige Diagramm zeigt Ihnen nur das Diagramm der Hyperbel, aber es gibt viele andere Elemente, die Sie beachten müssen, wie z. B. die schrägen Asymptoten, die Eckpunkte und die Brennpunkte. Überprüfen Sie die Grafik unten.
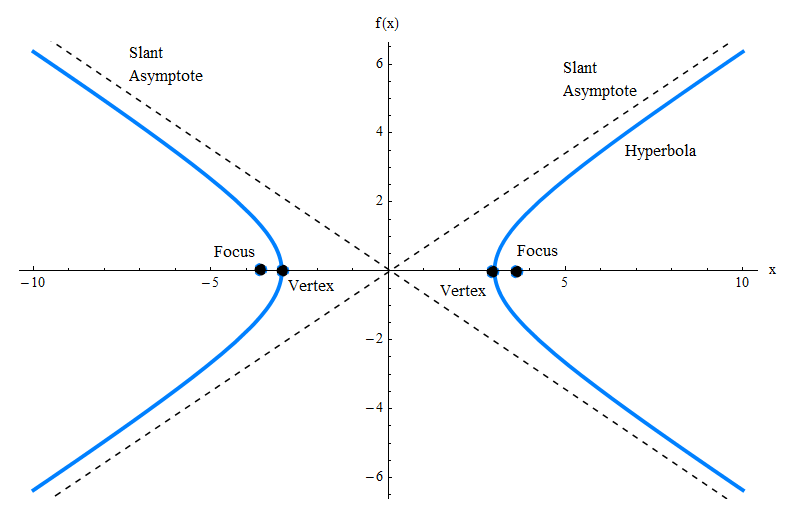
Die allgemeine Gleichung der Hyperbel
Ohne viel theoretische Diskussion werden wir feststellen, dass die allgemeine Gleichung der Hyperbel mit Brennpunkten auf der x-Achse lautet
\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
Für die durch die obige Gleichung beschriebene Hyperbel hat sie Eckpunkte an den Punkten \((-a, 0)\) und \((a, 0)\) und Brennpunkte an den Punkten \((-c, 0)\) und \((c, 0)\), wobei \(c = \sqrt{a^2 + b^2}\).
Ein interessantes Merkmal dieser Hyperbel ist, dass sie zwei schräge Asymptoten aufweist
Asymptote 1
: \(\displaystyle y = \frac{b}{a}x\)
Asymptote 2
: \(\displaystyle y = -\frac{b}{a}x\)
Was passiert nun mit der Gleichung der Hyperbel, wenn stattdessen die Eckpunkte durch einen bestimmten Punkt \((k,h)\) übersetzt werden?
In diesem Fall müssen Sie lediglich \(x\) durch \(x-k\) und \(y\) durch \(x-h\) ersetzen.
Wenn wir also eine Übersetzung machen, erhalten wir, dass die Gleichung einer allgemeinen Hyperbel lautet
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]Die obige Hyperbel hat Eckpunkte an den Punkten \((k-a, h)\) und \((k+a, h)\) und Brennpunkte an den Punkten \((k-c, h)\) und \((k+c, h)\), wobei \(c = \sqrt{a^2 + b^2}\).
Die Gleichungen der schrägen Asymptoten sind \(y = \frac{b}{a}(x-k) + h\) und \(y = -\frac{b}{a}(x-k) + h\).
Was passiert mit den Hyperbeln, die sich entlang der y-Achse öffnen?
Aus Symmetriegründen müssen wir lediglich die Rollen von \(x\) und \(y\) in der allgemeinen Gleichung der bereits vorhandenen Hyperbel ersetzen. In der Praxis bedeutet dies, dass überall dort, wo \(x\) in der Parabelgleichung vorkommt, \(y\) geändert wird und umgekehrt für \(y\).
Im Fall einer Hyperbel, die die x-Achse lang öffnet, lautet die allgemeine Gleichung
\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]Die obige Hyperbel hat Eckpunkte an den Punkten \((k, h - b)\) und \((k, h+b\) und Brennpunkte an den Punkten \((k, h-c)\) und \((k, h+c)\), wobei \(c = \sqrt{a^2 + b^2}\).
Die Gleichungen der schrägen Asymptoten sind \(y = \frac{b}{a}(x-k) + h\) und \(y = -\frac{b}{a}(x-k) + h\).
BEISPIEL 1
Finden Sie die Brennpunkte, Eckpunkte und schrägen Asymptoten der Hyperbel:
\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]ANTWORTEN:
Diese Hyperbel öffnet sich entlang der y-Achse. In diesem Fall sind die Übersetzungswerte \(k = 4\) und \(h = 2\). Außerdem erhalten wir \(a = \sqrt{16} = 4\) und \(b = \sqrt{9} = 3\). Daher erhalten wir das \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).
Daher sind die Schwerpunkte \((k, h-c) = (4, 2 - 5) = (4, -3)\) und \((k, h+c) = (4, 2 + 5) = (4, 7)\).
Die Eckpunkte sind \((k, h-b) = (4, 2 - 3) = (4, -1)\) und \((k, h+b) = (4, 2 + 3) = (4, 5)\).
Die schrägen Asymptoten sind
\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]Grafisch:
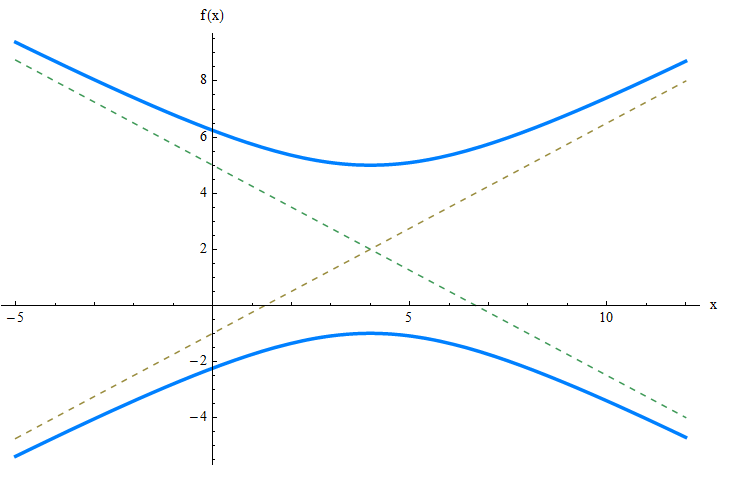
BEISPIEL 2
Finden Sie die Gleichung der Hyperbel mit den Brennpunkten am Scheitelpunkt \((-4, 0)\) und \((4, 0)\), konzentrieren Sie sich auf \((6, 0\).
ANTWORTEN:
Beachten Sie, dass sich die Brennpunkte und Scheitelpunkte auf der x-Achse befinden, sodass sich die Hyperbel entlang der x-Achse öffnet. Da die Brennpunkte in Bezug auf den Ursprung symmetrisch sind und ein Scheitelpunkt \((4, 0)\) ist, erhalten wir diesen \(a = 4\). Und da ein Fokus auf \((6, 0)\) liegt, erhalten wir diesen \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).
Daher lautet die Gleichung der Hyperbel:
\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]Die Hyperbel- und allgemeinen Kegelschnitte
Wie bei der Parabel ist die Hyperbel eng mit dem Kegel verbunden. In der Tat ist ein griechischer Mathematiker namens Apollonius derjenige, der diesen Zusammenhang entdeckt hat, indem er das Konzept der Kegelschnitte verstanden hat.
Ein Kegelschnitt tritt auf, wenn Sie einen Kegel mit einer Ebene schneiden. Abhängig vom relativen Winkel des Kegels und der Ebene am Schnittpunkt wird der Kegel so geschnitten, dass der Querschnitt eine bestimmte Form hat .
Abhängig vom relativen Schnittwinkel haben wir also unterschiedliche Formen des Abschnitts, und dies sind Parabel, Kreis, Ellipse und Hyperbel. Siehe die Grafik unten:
Mehr über die Hyperbel
Eine Hyperbel mit einem Scheitelpunkt am Ursprung, der sich entlang der x-Achse öffnet, hat die Gleichung \(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \), während eine Hyperbel, die sich entlang der y-Achse öffnet, die Gleichung \(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1 \) hat.
Dann kann ein allgemeiner Scheitelpunkt erhalten werden, indem einfach eine Übersetzung auf einen gegebenen Punkt \((k, h)\) angewendet wird.
Anwendungen
Die Hyperbel hat viele Anwendungen in der praktischen Welt sowie in der Astronomie. Ein Unterschied zur Parabel besteht darin, dass die Hyperbel schräge Asymptoten aufweist, die die Parabel nicht hat.
Algebraisch gesehen ähnelt eine Hyperbel einer Ellipse viel mehr als einer Parabel, obwohl der Unterschied im Vorzeichen mit der Ellipse einen großen Unterschied in Form und Eigenschaften bewirkt.
Eine weitere wichtige Art von Kegelschnitt ist die Parabel, über die Sie hier lernen können Lernprogramm . Sie können auch alles lernen, was es zu tun gibt lerne etwas über den Kreis und die Ellipse .