Löser Statistiken

Binomial-Erweiterungsrechner

Anweisungen: Sie können diesen Binomial-Koeffizientenrechner verwenden, um den Schritt für Schritt zu erläutern, wie Sie die Erweiterung für \((a + b)^n\) erhalten. Bitte geben Sie die Werte von \(a\), \(b\) und \(n\) ein:

Was Sie über diesen Binomial-Erweiterungsrechner wissen möchten

Dieser Binomial-Erweiterungsrechner mit Schritten bietet Ihnen eine klare Show, wie der Ausdruck berechnet wird \[(a+b)^n\]

Für die angegebenen Zahlen \(a\), \(b\) und \(n\), wobei \(n\) eine ganze Zahl ist.Der obige Ausdruck kann in einer Reihenfolge berechnet werden, die aufgerufen wird Die Binomial-Erweiterung und es hat viele Anwendungen in verschiedenen Bereichen von Mathematik.

Die Binomial-Erweiterung der Bestellung n

Mit diversen Ansätzen wurde die Formel für eine Binomial-Erweiterung gefunden, und es ist wie unten gezeigt

\[(a+b)^n = a^n + \dbinom{n}{1} a^{n-1} b + \dbinom{n}{1} a^{n-2} b^2 + ... \dbinom{n}{n-1} a b^{n-1} + b^n\]

wo der Begriff \(\dbinom{n}{k}\) berechnet ist:

\[\dbinom{n}{k} = \frac{n!}{k! \times (n-k)!}\]

Dieser Begriff \(\dbinom{n}{k}\) ist allgemein als k bekannt ^h Binomialkoeffizient einer Binomial-Erweiterung der Bestellung \(n\).Wie wir sehen können, a Binomialerweiterung der Reihenfolge \(n\) hat \(n+1\) Begriffe, wenn \(n\) eine positive ganze Zahl ist.

Pascal-Dreieck für einen Binomial-Expansionsrechner Negative Leistung

Eine sehr klugere und einfache Möglichkeit, die Koeffizienten einer Binomial-Erweiterung zu berechnen, ist, ein Dreieck zu verwenden, das mit "1" beginnt An der Spitze, dann "1" und "1" in der zweiten Reihe.Dann aus der dritten Reihe und auf dem Start "1" und "1" am Anfang und Ende von Die Zeile und die restlichen Koeffizienten können durch Hinzufügen der beiden obigen Elemente in der Zeile unmittelbar oben, wie in thakous gezeigt Diagramm unten.

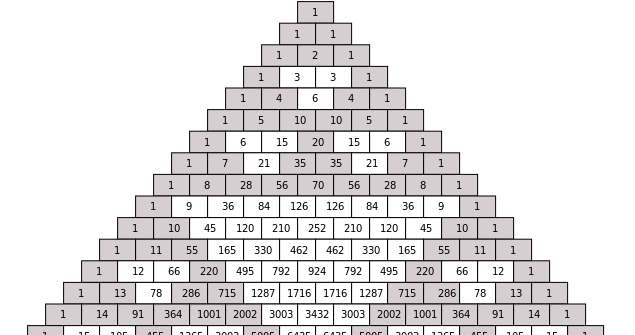
Ein Binomial-Erweiterungsrechner-Negativmächte

Bisher haben wir in Betracht gezogen, dass die Bestellung \(n\) eine positive ganze Zahl ist, aber es gibt auch eine Erweiterung, wenn \(n\) negativ ist, nur das ist nicht unbedingt Finite, und es wird in der allgemeinen Falle eine unendliche Anzahl von Begriffen beinhalten.