Mais sobre este gerador de gráfico quadrático

Esta calculadora de gráfico quadrático permitirá que você gere o gráfico para qualquer função quadrática que você fornecer. Pode ser qualquer função quadrática válida, por exemplo, x^2 - 3x + 1/2, mas você também pode fornecer uma função quadrática que não seja simplificada, como x^2 - 3x - 4 - 1/2 x^2 - 1/5, desde que seja uma função quadrática válida.

Depois de fornecer uma expressão quadrática válida, você pode clicar no botão "Calcular" e o gráfico da função será gerado, mostrando as etapas do cálculo do vértice da parábola e a Eixo de simetria também .

As funções quadráticas têm um papel predominante na álgebra básica, pois são frequentemente usadas no contexto da solução de equações quadráticas e problemas de aplicação. Eles são essencialmente básicos polinômios , que têm muitas propriedades interessantes.

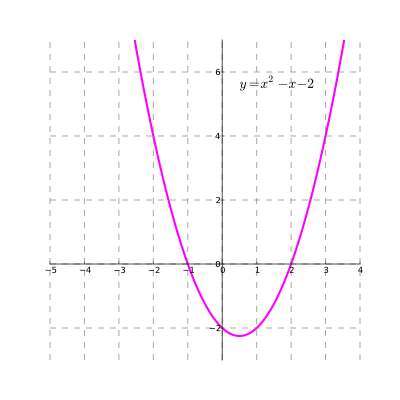
Como fazer gráficos de segundo grau?

Fazer um gráfico quadrático é simples, no sentido de que você sabe que TODAS as funções quadráticas terão a forma de uma parábola. Mas ainda existem parábolas infinitas. Precisamos saber um pouco mais para identificar a parábola precisa que representa uma dada função quadrática.

Etapas para encontrar um gráfico de função quadrática

• Passo 1: Identifique claramente a função quadrática dada e simplifique se necessário
• Passo 2: Após a simplificação, identifique a função na forma f(x) = ax² + bx + c. Observe que a não pode ser zero
• Passo 3: Se a > 0, você sabe que o gráfico será uma parábola com concavidade para cima, enquanto se a < 0, você sabe que o gráfico será uma parábola com concavidade para baixo
• Etapa 4: o eixo de simetria está em x* = -b/(2a), o que indica o 'centro' da parábola
• Etapa 5: Observe que x* = -b/(2a) é a coordenada x do vértice da parábola e y* = f(x*) = a(x*)² + b(x*) + c é a coordenada y do vértice

Isso deve ser suficiente para ter uma ideia clara sobre o gráfico quadrático correspondente. Um outro passo seria plotar alguns pontos no gráfico, escolhendo diferentes pontos no eixo x e encontrando sua imagem correspondente através da função, de forma a auxiliar o processo de encontrar o gráfico da função .

A fórmula quadrática

É o Fórmula quadrática relacionado com o gráfico de uma função quadrática? Pode apostar! Geometricamente falando, ao resolver a equação quadrática

$$a x^2 + bx + c = 0$$

você obtém as raízes da equação quadrática e, quando as raízes são reais, elas representam os pontos onde a parábola cruza o eixo x.

Um caso especial ocorre quando as raízes são complexas, caso em que a parábola não cruzará o eixo x.

Tipos de gráficos quadráticos

Como mencionamos antes, TODAS as funções quadráticas univariadas serão representadas por parábolas, mas dependendo se a > 0 ou a < 0, as parábolas se abrirão para cima ou para baixo, respectivamente.

Outra distinção dos tipos de parábolas poderia ser para aquelas que são "centradas" (ou seja, as vértice é a origem), e aqueles que não são.

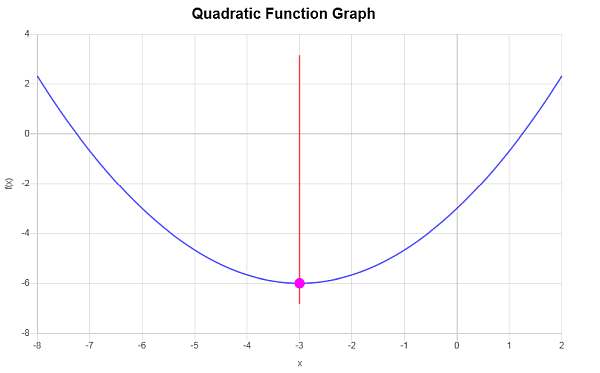
Exemplo: gráfico quadrático

Construa o gráfico de: $f(x) = \frac{1}{3}x^2 +2x - 3$

Solução:

Precisamos representar graficamente a função quadrática fornecida $f(x) = \displaystyle \frac{1}{3}x^2+2x-3$. Além disso, as coordenadas do vértice serão computadas.

Para uma função quadrática da forma $f(x) = a x^2 + bx + c$, a coordenada x do vértice é calculada usando a seguinte fórmula:

$$x_V = \displaystyle -\frac{b}{2a}$$

Nesse caso, temos que a função para a qual precisamos encontrar o vértice é $f(x) = \displaystyle \frac{1}{3}x^2+2x-3$, o que implica que os coeficientes correspondentes são:

$$a = \frac{1}{3}$$ $$b = 2$$ $$c = -3$$

Colocando os valores conhecidos de $a$ e $b$ na fórmula para a coordenada x do vértice, obtemos:

$$x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3$$

Agora, precisamos inserir o valor de $x_V = \displaystyle -3$ na função quadrática, então obtemos:

$$y_V = f(x_V)$$ $$= \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6$$

Portanto, a coordenada x do vértice é $x_V = \displaystyle -3$ e a coordenada y do vértice é $y_V = \displaystyle -6$. Isso indica que o ponto que representa o vértice é $\displaystyle \left(-3, -6\right)$.

O seguinte é obtido graficamente:

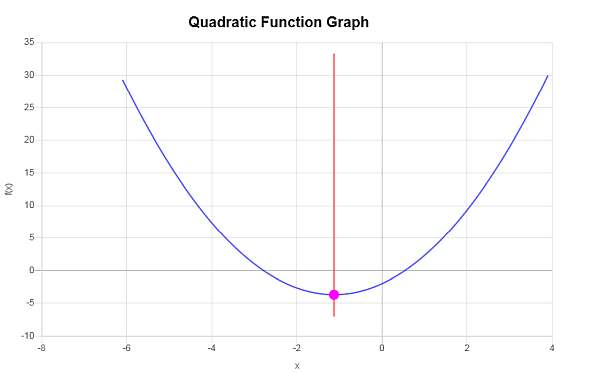
Exemplo: gráfico quadrático

Gráfico: $f(x) = \frac{4}{3}x^2 +3x - 2$, que tipo de gráfico quadrático é esse?

Solução: Nesse caso, temos que a função para a qual precisamos encontrar o vértice é $f(x) = \displaystyle \frac{4}{3}x^2+3x-2$, o que implica que os coeficientes correspondentes são:

$$a = \frac{4}{3}$$ $$b = 3$$ $$c = -2$$

Colocando os valores conhecidos de $a$ e $b$ na fórmula para a coordenada x do vértice, obtemos:

$$x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}$$

Agora, precisamos inserir o valor de $x_V = \displaystyle -\frac{9}{8}$ na função quadrática, então obtemos:

$$y_V = f(x_V)$$ $$= \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}$$

Portanto, a coordenada x do vértice é $x_V = \displaystyle -\frac{9}{8}$ e a coordenada y do vértice é $y_V = \displaystyle -\frac{59}{16}$. Isso indica que o ponto que representa o vértice é $\displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)$.

O seguinte é obtido graficamente:

Mais calculadoras quadráticas

Quase todas as aplicações em Álgebra básica são baseadas na resolução de algum tipo de Equação quadrática , por isso tem um forte propósito pedagógico de aprender sobre isso.

O Fórmula quadrática é um dos objetos ensináveis mais notórios em matemática. Não é que não existam equações cúbicas ou quárticas, é que equações quadráticas são os que podemos explicar facilmente.