Mais sobre este gráfico de equações lineares

Traçar linhas é uma habilidade fundamental e esta calculadora irá ajudá-lo com isso. Você precisa começar fornecendo o equação linear você deseja fazer o gráfico.

Você pode fornecer qualquer equação linear explicitamente, por exemplo, x + 3y = 2 , ou algo que não seja totalmente simplificado como x + 3y = 2/3 x.

Linhas gráficas tem tantas aplicações, que se torna uma habilidade muito prática de adquirir. Geometricamente, as linhas têm uma intuição muito simples que facilita a representação gráfica, pois não precisamos de muitas informações para especificá-las.

Como representar graficamente equações lineares?

você pode usar isso calculadora gráfica para traçar linhas. Caso opte por fazer manualmente, é preciso estar ciente de que a abordagem requer um preâmbulo que dependerá do tipo de informação fornecida.

Quais são as etapas para representar graficamente uma linha?

• Passo 1: Identifique o tipo de informação fornecida. Você tem uma equação real fornecida, você tem dois pontos, um ponto e a inclinação, inclinação e interceptação em y? Avalie com clareza
• Etapa 2: Independentemente das informações fornecidas, use-as para encontrar dois pontos por onde a linha passa. Para uma equação dada, resolva y para x = 0 e x = 1, por exemplo. Para inclinação e interceptação y, você constrói a equação y = a + bx e encontra dois pontos. Se você tiver um ponto e inclinação, defina y = y1 + b(x-x1) e conecte-o em x = 0
• Etapa 3: depois de ter dois pontos por onde a linha passa, use uma régua para traçar uma linha passando por eles

As linhas são super fáceis de desenhar, basta você ser metódico e estar atento ao tipo de informação que tem disponível.

Mesmo se você fizer isso à mão, é sempre bom ter um linear à mão calculadora gráfica online para verificar seus resultados.

Linhas gráficas

A representação gráfica de linhas tem muitas aplicações. Por exemplo, você pode resolver um sistema de equações traçando as linhas correspondentes e vendo onde elas se cruzam.

Usando esse método, quando as linhas são paralelas e não se cruzam, não haverá soluções.

Semelhante ao que aconteceu com adição e subtração, a divisão de frações é derivada apenas da multiplicação de frações: Para dividir duas frações, basta multiplicar a primeira pela fração inversa da segunda (a fração inversa é obtida trocando o numerador pelo denominador na fração).

Outras aplicações de gráficos lineares

Linhas ou Gráficos lineares estão verdadeiramente presentes em todos os lugares. funções lineares aparecem em aplicativos o tempo todo, em Cálculo e Otimização, por isso são realmente úteis.

Exemplo: exemplo de gráfico de equação linear

Faça o gráfico das seguintes equações: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Solução: Devemos trabalhar com a seguinte equação:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Trabalhando primeiro com as constantes:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

O resultado é obtido colocando (y) no lado esquerdo e (x) e a constante no lado direito:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Em seguida, o processo continua resolvendo para \(y\) e, em seguida, dividindo ambos os lados da equação por \(\frac{7}{4}\). Obtemos então:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

e após a simplificação, o resultado é o seguinte.

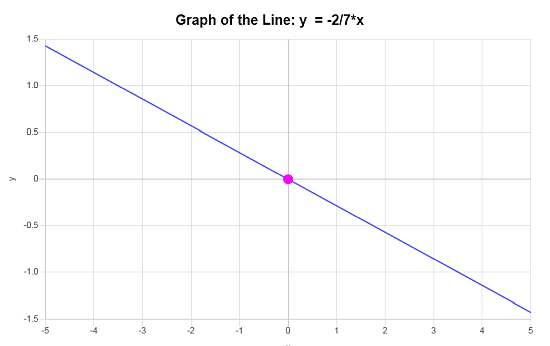
\[\displaystyle y=-\frac{2}{7}x\]

Conclusão : Inferimos que a equação da linha na forma de interceptação de inclinação baseada nos dados disponíveis é \(\displaystyle y=-\frac{2}{7}x\), com uma inclinação de \(\displaystyle b = -\frac{2}{7}\) e interceptação y de \(\displaystyle n = 0\).

Portanto, o gráfico da linha fornecida é

Exemplo: exemplo de gráfico de equação linear

Obtenha a linha que representa: \(\frac{2}{3}x + \frac{5}{4}y = - \frac{5}{6}x + 2\)

Solução: Foi-nos fornecida a seguinte equação:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Trabalhando com as constantes:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Agora, colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito, obtemos

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Agora, o termo multiplicando \(y\) é \( \frac{5}{4} - 0 = \frac{5}{4}\), e também desde \( -\frac{5}{6} - \frac{2}{3} = -\frac{3}{2}\), obtém-se o seguinte

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Agora, resolvendo para \(y\), dividindo ambos os lados da equação por \(\frac{5}{4}\), obtém-se o seguinte

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

e simplificando, finalmente obtemos o seguinte

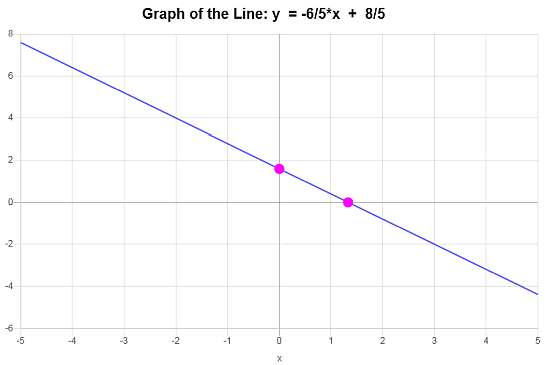
\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Conclusão : Com base nos dados fornecidos, concluímos que a equação da linha na forma inclinação-intersecção é \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), com uma inclinação de \(\displaystyle b = -\frac{6}{5}\) e intersecção y de \(\displaystyle n = \frac{8}{5}\).

O gráfico linear é

Mais calculadoras de linha

As linhas são tão importantes que merecem sua própria seção no livro de matemática. você pode calcular Equações Lineares em diferentes formas, dependendo das necessidades específicas.

Determinar as linhas, em última análise, precisará dois pontos por onde a linha passa , que podem ser dados direta ou indiretamente.