Sobre este gráfico de desigualdade

Esta calculadora irá ajudá-lo a encontrar a solução e o gráfico para qualquer desigualdade geral, mostrando todas as etapas. Você precisa fornecer uma desigualdade válida de uma variável (x), digitando-a na caixa fornecida.

Por exemplo, você pode fornecer uma desigualdade linear simples como '3x - 1 < 1/3', ou algo como '2x-x^2 <= 3/4', que corresponde a uma desigualdade quadrática.

Depois de fornecer a desigualdade que deseja representar graficamente, vá em frente e clique no botão “Resolver”, para que sejam apresentadas as soluções, com todos os passos, caso seja possível encontrar soluções.

Resolvendo equações gerais e as desigualdades gerais são em geral uma tarefa difícil, exceto para um conjunto específico de estruturas que são passíveis de um tratamento sistemático.

Alguns dos poucos tipos que permitem uma solução exata são desigualdades lineares e desigualdades polinomiais .

Um tipo importante de desigualdade que você gostaria de resolver é o caso das desigualdades racionais, nas quais você pode identificar um quociente de polinômios. Essas desigualdades são interessantes porque têm potenciais divisões por zero que precisam de ser abordadas. A ideia de uma desigualdade racional pode ser facilmente estendida ao quociente de funções em geral, não necessariamente polinômios

Como representar graficamente uma desigualdade

A resposta mais simples é: para representar graficamente uma inequação, você precisa saber como resolvê-la. A solução gráfica para uma inequação é geralmente representada como um intervalo ou vários intervalos unidos no eixo x.

Assim, dito isto, traçar o gráfico de uma inequação começará primeiro por resolvê-la, o que envolve encontrar um conjunto de valores na reta real que satisfaça a desigualdade fornecida.

Você pode potencialmente apresentar o gráfico como um intervalo independente ou pode representar graficamente as soluções da desigualdade junto com o gráfico da expressão que está subjacente à desigualdade: vamos lembrar isso para resolver desigualdades , você passa todos os termos para um lado (o que lhe dá a expressão subjacente) e resolve uma equação auxiliar

Etapas para resolver e representar graficamente desigualdades

• Passo 1: Passe todos os termos para um lado, então você terá uma expressão de um lado e zero do outro lado
• Passo 2: A partir da desigualdade (uma vez que tudo está de um lado e zero do outro), construa uma equação auxiliar
• Estágio 3: Resolva esta equação, com um método adequado à sua estrutura (diferentes tipos de equações exigirão técnicas e abordagens específicas)
• Passo 4: Com base nas soluções REAIS das equações auxiliares (reais em oposição às soluções complexas), você constrói seus pontos críticos e os classifica em ordem crescente
• Etapa 5: Você também precisa procurar pontos onde a expressão é indefinida. Um caso notável disso ocorre com desigualdades racionais, nas quais você tem um denominador que é um polinômio, então a expressão será indefinida nos zeros do denominador. Então você adiciona zeros do denominador à lista de pontos críticos
• Etapa 6: Com seus pontos críticos, você constrói intervalos usando pontos críticos consecutivos (usando -∞ e ∞ como pontos críticos iniciais e finais)
• Estágio 7: Para cada intervalo analise o sinal da expressão e veja se ele é compatível com o sinal da inequação. Se for, então o intervalo fará parte da solução geral para a desigualdade

Utilizar pontos críticos para a análise é de extrema importância, pois assim você tem certeza de que a expressão não muda de sinal dentro de cada intervalo, de modo que o problema se reduz a avaliar se a desigualdade é resolvida para cada um desses intervalos críticos.

Para tornar isso um pouco mais tangível, você tem alguma desigualdade dada e depois passa tudo para um lado, então você tem algo na forma \(f(x) \le 0\). Por exemplo, pode ser algo como \(x^2 - x + 1 \le 0\).

Então você pega \(f(x) \le 0\) e encontra a equação auxiliar \(f(x) = 0\). Você pega a expressão \(f(x)\) e descobre que seus zeros são os pontos críticos. Mas você não apenas faz isso, mas também verifica se \(f(x)\) está indefinido em algum lugar (divisões por zero, etc.). Talvez esteja definido em qualquer lugar, como no caso \(x^2 - x + 1\), mas se você encontrar pontos onde a expressão é indefinida, você o adiciona à lista de pontos críticos.

Então você constrói intervalos com base em pontos críticos consecutivos. Para \(f(x) \le 0\), você tomará como parte das soluções aqueles intervalos onde o valor da expressão é negativo. Se a desigualdade original fosse \(f(x) \ge 0\) você tomará como parte das soluções aqueles intervalos onde o valor da expressão é positivo

Como funciona este gráfico de desigualdade

Nosso gráfico de desigualdades online cuidará de um dos processos mais complicados da álgebra básica, que consiste em encontrar as soluções de uma desigualdade e representá-las graficamente. Uma grande vantagem da nossa calculadora é que ela mostrará todos os passos, quando possível.

Primeiro, o gráfico resolverá a desigualdade resolvendo primeiro uma equação auxiliar adequada. Este processo requer a detecção de estruturas conhecidas específicas, pois todas as estruturas provavelmente requerem abordagens diferentes. Por exemplo, para resolver uma desigualdade racional (que envolve o quociente de dois polinômios) como por exemplo

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

você precisará de uma abordagem diferente daquela usada para resolver uma desigualdade quadrática como \(x^2 + 3x < 1\), por exemplo, e esta calculadora analisará todos esses detalhes

Se nenhuma estrutura tradicional ou comumente conhecida for detectada, serão utilizadas diferentes substituições comumente usadas, como por exemplo \(u = \sqrt x\) ou \(u = \sin x\). Se nada funcionar, a calculadora tentará encontrar soluções por inspeção e numericamente, para ter pelo menos uma ideia das soluções.

Como você apresenta um gráfico de desigualdade?

Como mencionamos acima, não está realmente escrito em pedra, mas a forma mais comum é representar graficamente a expressão subjacente da desigualdade e destacar os valores de x que satisfazem a desigualdade. Este é possivelmente o melhor formato gráfico para isso, e é o que é usado por este gráfico.

Você também pode desenhar um objeto de intervalo independente, mas isso é possivelmente menos revelador, pois perde a perspectiva do que realmente está acontecendo com a própria desigualdade.

Exemplo: representando graficamente desigualdades

Faça um gráfico da seguinte desigualdade: \(\frac{1}{x}+x > 1\)

Solução: Temos a seguinte desigualdade que precisa ser resolvida:

\[\frac{1}{x}+x > 1\]

Precisamos colocar todos os termos da desigualdade de um lado:

\[x+\frac{1}{x}-1>0\]

Resolvendo equação auxiliar

Da desigualdade acima, obtemos a equação associada que precisa ser resolvida primeiro:

\[x+\frac{1}{x}-1=0\]

Análise de pontos críticos

Precisamos organizar os pontos críticos encontrados (a partir das raízes reais do numerador e do denominador) em ordem crescente, definir intervalos com todos os pontos críticos consecutivos e avaliar o sinal do tamanho esquerdo da desigualdade em cada um desses intervalos .

O único ponto crítico encontrado é \(0\).

Com base nisso, precisamos analisar os seguintes intervalos:

• Para o intervalo \(\left(-\infty, 0\right)\): O numerador é positivo e o denominador é negativo, então o lado esquerdo é negativo, o que implica que \(\left(-\infty, 0\right)\) não faz parte da solução.

• Para o intervalo \(\left(0, \infty\right)\): O numerador é positivo e o denominador é positivo, então o lado esquerdo é positivo, então \(\left(0, \infty\right)\) faz parte da solução.

Solução para a desigualdade

Com base na desigualdade fornecida e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x > 0\).

Usando a notação de intervalo, a solução é escrita como:

\[\left(0,\infty\right)\]

O seguinte é obtido com o gráfico de desigualdade:

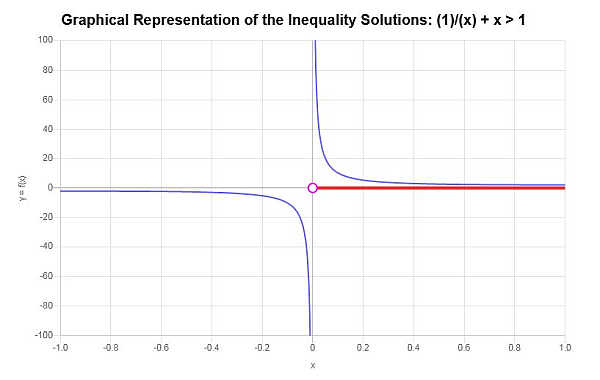
que conclui o cálculo.

Exemplo: representando graficamente desigualdades polinomiais

Encontre o gráfico da desigualdade: \(x^2 - 2x \ge 4\)

Solução:

Precisamos colocar todos os termos da desigualdade de um lado:

\[x^2-2x-4\ge0\]

Resolvendo equação auxiliar

Da desigualdade acima, obtemos a equação associada que precisa ser resolvida primeiro:

\[x^2-2x-4=0\]

Usando a fórmula quadrática

Para uma equação quadrática da forma \(a x^2 + bx + c = 0\), as raízes são calculadas usando a seguinte fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos que a equação que precisamos resolver é \(\displaystyle x^2-2x-4 = 0\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = -2\] \[c = -4\]

Primeiro, calcularemos o discriminante para avaliar a natureza das raízes. A discriminação é calculada como:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle 20 > 0\), que é positivo, sabemos que a equação tem duas raízes reais diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

então, descobrimos que:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

Neste caso, a equação quadrática \( \displaystyle x^2-2x-4 = 0 \), possui duas raízes reais, então:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

então o polinômio original é fatorado como \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), o que completa a fatoração.

Análise de pontos críticos

A lista de pontos críticos encontrados organizados em ordem crescente é: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

Com base nisso, precisamos analisar os seguintes intervalos:

• Para o intervalo \(\left(-\infty, -\sqrt{5}+1\right)\): O lado esquerdo é positivo, então \(\left(-\infty, -\sqrt{5}+1\right)\) faz parte da solução.

• Para o intervalo \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): O lado esquerdo é negativo, então \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) não faz parte da solução.

• Para o intervalo \(\left(\sqrt{5}+1, \infty\right)\): O lado esquerdo é positivo, o que implica que \(\left(\sqrt{5}+1, \infty\right)\) faz parte da solução.

Solução para a desigualdade

Com base na desigualdade fornecida, e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x \le -\sqrt{5}+1\) ou \(x \ge \sqrt{5}+1\).

Usando a notação de intervalo, a solução é escrita como:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Graficamente:

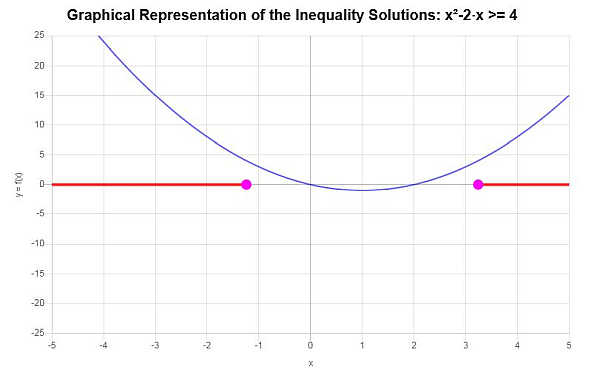
que conclui o cálculo.

Mais calculadoras de álgebra

À medida que você avança no aprendizado de Álgebra e Cálculo, você provavelmente percebeu lentamente que Resolvendo equações desempenhar um papel crucial. E à medida que você aprende mais, você percebe que às vezes temos menos informações e acabamos nos deparando com o problema de Resolvendo Desigualdades .

Em essência, resolver desigualdades não é mais difícil do que resolver equações, bastando apenas alguns passos mais organizados. O principal problema é que não podemos realmente resolver a maioria das equações, pelo menos com exatidão.

E mesmo resolvendo equações numericamente, ainda não temos boas maneiras de garantir que encontramos TODAS as soluções para TODAS as equações possíveis. Algumas equações notáveis que podem ser resolvidas e aparecem em aplicações o tempo todo são as equações polinomiais , que você pode resolver usando principalmente métodos padrão (mas apenas para polinômios de grau inferior)

Um dos tipos de desigualdades mais comumente questionados que você precisa resolver em seus testes de matemática são as desigualdades racionais, porque são as desigualdades simples mais difíceis que você pode garantir que encontrará uma solução (desde que os graus envolvidos sejam baixos o suficiente, ou os polinômios são bastante simples).