Resolvendo equações radicais

Este solucionador de equações radicais permite lidar com equações radicais fornecidas, manipulando-as algebricamente enquanto mostra todas as etapas do processo.

Este solucionador aceitará qualquer equação válida envolvendo raízes, como algo realmente simples como 'sqrt(x) = 1', ou algo que pode ser muito mais difícil de resolver como 'sqrt(x+3) = x^2 - 1'.

Depois que uma equação radical válida for fornecida, você estará basicamente pronto e tudo o que resta fazer é clicar em "Resolver" para obter todas as etapas do processo mostradas.

A solução da equação radical forte depende de eficiência manipulação algébrica da expressão , para basicamente se livrar da parte radical.

O que é equação radical

Uma equação radical, colocada em termos extremamente simples, é um tipo de equação matemática em que a incógnita (normalmente x) está dentro de um radical. Por exemplo

\[\displaystyle \sqrt x = x^2 \]

é uma equação radical, por causa do termo \( \sqrt x\), mas a equação

\[\displaystyle 2 x = x^2 \]

por exemplo, NÃO é uma equação radical, porque não podemos x estar dentro de um radical em qualquer lugar da equação.

Como resolver equações radicais

Resolver equações radicais não é difícil se você seguir estas etapas:

Às vezes, independentemente do agrupamento e da simplificação apropriados, não será possível eliminar totalmente os radicais ou levará a uma equação ainda mais complicada.

Simplificando equações radicais

Como mencionamos acima, o sucesso do cálculo de equações envolvendo raízes depende fortemente da capacidade de simplificar radicais . Mas às vezes isso não será suficiente, pois simplificar todos os radicais que ocorrem não os fará desaparecer. A maneira mais comum é reduzir os radicais e depois aplicar o quadrado (potência de 2) para cancelar o radical.

Mas elevar ao quadrado para eliminar o radical é uma faca dupla, porque ao elevar ao quadrado qualquer sinal relevante pode desaparecer. É isso que ao “eliminar” o radical e encontrar soluções de uma equação auxiliar, DEVEMOS verificar novamente se as soluções auxiliares também são soluções da equação original. Muitas vezes não são.

Outra forma de ver o processo de eliminação do radical é utilizando uma substituição adequada. Por exemplo, para a equação radical:

\[\displaystyle \sqrt x = x \]

você pode querer definir \(u = \sqrt x\), então \(u^2 = (\sqrt x)^2 = x\), então a equação original se transforma na seguinte equação auxiliar:

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

que é uma equação polinomial que podemos resolver. Então, usar uma substituição leva de uma equação que não sabemos como resolver, para resolvendo uma equação polinomial que sabemos quem resolver.

Por que nos preocupamos com equações radicais?

Equações radicais são aparências comuns em Álgebra e Cálculo, pois são a base para modelar tantos fenômenos diferentes.

As funções radicais são interessantes em termos de suas propriedades e tipo de crescimento lento à medida que x se aproxima do infinito.

Exemplo: resolvendo equações envolvendo radicais

Resolva o seguinte: \(\sqrt{x} = 2x\)

Solução:

Temos a seguinte equação. Precisamos resolver essa equação que possui apenas uma variável, que é \(x\), então o objetivo é resolver para \(x\):

\[\sqrt{x}=x^2\]

Observe que o grau do polinômio dado é \(\displaystyle deg(p) = 4\), seu coeficiente líder é \(\displaystyle a_{4} = -1\) e seu coeficiente constante é \(\displaystyle a_0 = 0\).

Tentando raízes racionais

Candidatos A Raízes Racionais : Como o primeiro termo com coeficiente diferente de zero em \(p(x)\) é \(x\), podemos fatorar esse termo para obter

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

mas o termo entre parênteses tem grau maior que 2, então não existe uma fórmula elementar para fatorá-lo. Precisamos testar possíveis raízes racionais.

A próxima tarefa é encontrar os números inteiros que dividem o coeficiente líder \(a_{3}\) e o coeficiente constante \(a_0\), que serão usados para construir nossos candidatos a zeros da equação polinomial.

Portanto, dividindo cada divisor do coeficiente constante \(a_0 = 1\) por cada divisor do coeficiente líder \(a_{3} = -1\), encontramos a seguinte lista de candidatos a raízes:

\[\pm \frac{ 1}{ 1}\]

Agora, todos os candidatos precisam ser testados para ver se são uma solução. O seguinte é obtido a partir do teste de cada candidato:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

Divisão Polinomial : Como não temos raízes suficientes entre os candidatos racionais, dividiremos \(\displaystyle -x^3+1\) pelo produto dos fatores derivados das raízes racionais, que é \(\displaystyle \left(x-1\right) \).

Passo 1: O termo inicial do dividendo \(\displaystyle p(x) = -x^3+1\) é \(\displaystyle -x^3\), enquanto o termo inicial do divisor \(\displaystyle s(x) = x-1\) é igual a \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo principal do dividendo é \(\displaystyle \frac{ -x^3}{ x} = -x^2\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), que precisamos subtrair ao dividendo:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

Passo 2: Agora, o termo inicial do restante atual \(\displaystyle -x^2+1\) é \(\displaystyle -x^2\), e sabemos que o termo inicial do divisor é \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo inicial do resto atual é \(\displaystyle \frac{ -x^2}{ x} = -x\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), que precisamos subtrair ao lembrete atual:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

Estágio 3: Agora, o termo inicial do restante atual \(\displaystyle -x+1\) é \(\displaystyle -x\), e sabemos que o termo inicial do divisor é \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo inicial do resto atual é \(\displaystyle \frac{ -x}{ x} = -1\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), que precisamos subtrair ao lembrete atual:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

Portanto, o quociente é \(\displaystyle q(x) = -x^2-x-1\) e o resto é \(\displaystyle r(x) = 0\).

Então, depois de dividir, avançamos na fatoração com

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

Mas agora, como o quociente encontrado \(\displaystyle -x^2-x-1\) é quadrático, podemos determinar as suas raízes para ver se conseguimos fatorá-lo no campo real.

Precisamos resolver a seguinte equação quadrática \(\displaystyle -x^2-x-1=0\).

Usando a fórmula quadrática

Para uma equação quadrática da forma \(a x^2 + bx + c = 0\), as raízes são calculadas usando a seguinte fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos que a equação que precisamos resolver é \(\displaystyle -x^2-x-1 = 0\), o que implica que os coeficientes correspondentes são:

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle -3 < 0\), que é negativo, sabemos que a equação dada tem duas raízes complexas conjugadas diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

então, descobrimos que:

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

Assim, após encontrar as raízes da última parte quadrática, encontramos duas raízes complexas, portanto não podemos fatorar o termo \(-x^2-x-1\) no corpo real, então finalizamos o processo com \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).

Portanto, resolver \(x\) para a equação polinomial dada leva às soluções \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), usando métodos de fatoração.

Verificando as soluções auxiliares

Testar essas soluções a partir da equação polinomial auxiliar mostra que nem todas as soluções candidatas são de fato uma solução da equação original. As únicas soluções reais para a equação original são:

\[x_1=0 \]
\[x_2=1 \]

Portanto, resolver \(x\) para a equação dada leva às soluções \(x=0,\,\,x=1\).

Graficamente

A seguir está a representação gráfica das soluções obtidas:

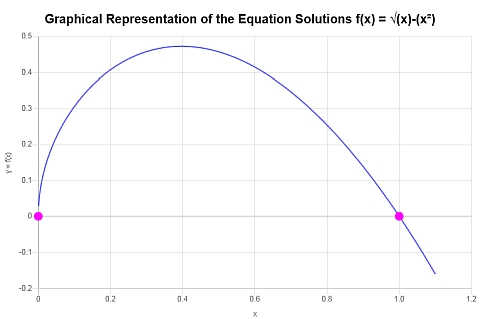
que conclui o cálculo.

Outros solucionadores de equações úteis

Ao resolver equações radicais, ao contrário do caso de quando você precisa Resolver equações lineares ou quando você precisar resolver uma equação quadrática , se enquadra na categoria daquelas equações que requerem manipulação algébrica tão inteligente para resolver x.

Em outras palavras, você não terá uma coisa do tipo “faça assim e sempre funcionará”. O tipo de manipulação que você realizará dependerá da estrutura da equação e pode variar muito de caso para caso.

simplificando expressões primeiro é sempre uma boa prática, porque você reduzirá os termos que podem estar atrapalhando a estrutura geral da equação.