Usando la regola dei segni di cartesio

Questo calcolatore ti aiuterà con l'applicazione della regola dei segni di Descartes, per ogni dato polinomio che fornisci. L'unico requisito è che il polinomio deve essere valido.

Ad esempio, puoi fornire un semplice polinomio cubico come x^3 - 2x + 1, ma puoi anche fornirne uno più complicato, come x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^ 2 + 2x + 1, ecc.

Una volta fornito un file valido funzione polinomiale , fai clic sul pulsante "Calcola", per ottenere tutti i passaggi del processo mostrato.

Trovare zeri polinomiali è uno dei compiti più importanti in Algebra, ma non è un compito facile in generale. Non ci sono formule generali per tutti i polinomi di tutti i gradi, quindi di solito dobbiamo seguire una procedura sistematica per trovare quante più radici possibile.

In questo contesto, è sempre utile disporre di quante più informazioni sul tipo di radici disponibili, e questo è uno degli obiettivi della Regola dei segni di Cartesio.

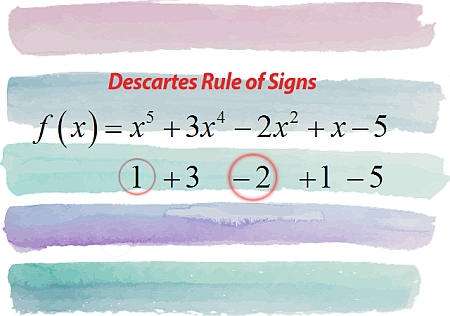
Cosa afferma la regola dei segni di cartesio?

In termini semplici, la regola dei segni di Descartes ti dice qualcosa sul numero di radici positive e negative di un polinomio, semplicemente osservando i segni dei coefficienti del dato polinomio.

Più precisamente, inizi con il coefficiente principale, ignori zero coefficienti e conti i cambiamenti di segno. Il numero totale di cambiamenti nel segno di coefficienti consecutivi è un limite superiore per il numero di radici positive di \(p(x)\), e il numero di radici positive ha la stessa parità del numero totale di cambiamenti di segno.

Quindi, fai lo stesso esercizio, ma per i coefficienti di \(p(-x)\), e quello che ottieni in quel caso è che il numero totale di cambiamenti nel segno di coefficienti consecutivi è un limite superiore per il numero di radici negative di < > e il numero di radici negative ha la stessa parità del numero totale di cambi di segno.

Passaggi per l'applicazione della regola dei segni di cartesio

• Fase 1: Identifica il polinomio p(x) che devi analizzare. Assicurati che sia un polinomio (altrimenti il metodo non funziona) e semplificalo il più possibile
• Passo 2: Metti in fila i coefficienti di p(x), partendo dal coefficiente principale, in ordine decrescente e omettendo zero coefficienti
• Smusso 3: Partendo dal coefficiente principale, conta i cambi di segno tra coefficienti consecutivi e prendi nota del numero totale di cambi di segno e chiamalo T
• Passaggio 4: Il numero di zeri positivi di p(x) è al massimo T e ha la stessa parità di T (se T è pari, allora il numero di zeri positivi di p(x) è pari, e se T è dispari, allora il numero di zeri positivi di p(x) è un numero dispari)
• Passaggio 4: Ripeti ora lo stesso processo per i coefficienti di p(-x), per ottenere informazioni sul numero di zeri negativi di p(x)

Questo metodo può darti potenzialmente un intervallo di possibili valori per il numero di zeri positivi (e negativi), ma può anche potenzialmente dirti ESATTAMENTE quanti zeri positivi (o negativi) ha un dato polinomio, a seconda solo di quanti segni cambiano tu conti.

Posso calcolare gli zeri effettivi con questo metodo?

No, la regola dei segni di Descartes non ha lo scopo di darti informazioni su quali siano le radici effettive, ti dice solo qualcosa sul NUMERO di radici positive (e negative).

Ora, combinando queste informazioni, con il teorema della radice razionale e altri strumenti elementari, tra cui Divisione sintetica e il teorema dei fattori , sarai meglio attrezzato per osservare il valore effettivo delle radici.

Suggerimenti e trucchi

Sempre semplificare prima il polinomio. Ad esempio, se hai \(p(x) = x^5 - x^3\), vorrai prima \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\), quindi sai che 0 è una radice (con molteplicità 3) e applichi la regola di Descartes a \(x^2 - 1\) Invece.

Esempio: regola dei segni di cartesio

Indicare il possibile numero di radici positive e negative di \(x^4 - x^3 + x^2 + 1\)

Soluzione: Ci viene fornita la seguente funzione polinomiale: \(\displaystyle x^4 - x^3 + x^2 + 1\), per la quale dobbiamo applicare la regola dei segni di Cartesio.

Radici Positive : I coefficienti polinomiali (dalla potenza maggiore alla minore) sono:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

Troviamo che il numero di cambi di segno in coefficienti consecutivi è: \(2\), e i cambi sono: \(\,\,+1\,\,\) e\(\,\,-1\,\,\), \(\,\,-1\,\,\) e\(\,\,+1\,\,\).

Radici Negative : I coefficienti polinomiali per \(p(-x) = x^4+x^3+x^2+1\) sono:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

Non si riscontrano variazioni di segno per i coefficienti di \(p(-x)\).

Conclusione: Sulla base del numero di cambi di segno trovati, che è \(2\), concludiamo che \(p(x)\) può avere 0 o 2 radici positive per \(p(x) = x^4-x^3+x^2+1\).

Ora, poiché non sono stati trovati cambiamenti di segno per i coefficienti di \(p(-x)\), concludiamo che NON ci sono zeri negativi per \(p(x) = x^4-x^3+x^2+1\).

Esempio: più della regola del segno di cartesio

Indicare il possibile numero di radici positive e negative di \(x^4 + x^3 + x^2 - 1\)

Soluzione: Ora dobbiamo analizzare \(\displaystyle x^4 + x^3 + x^2 - 1\), con la regola dei segni di Descartes.

L'espressione fornita è già semplificata, quindi non c'è altro da semplificare.

Radici Positive : I coefficienti sono:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Si osservi che il numero di cambi di segno in coefficienti consecutivi in questo caso è uguale a \(1\), e i cambi sono: \(\,\,+1\,\,\) e\(\,\,-1\,\,\).

Radici Negative : I coefficienti polinomiali associati a \(p(-x) = x^4-x^3+x^2-1\) sono:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Quindi, il numero di cambi di segno in coefficienti consecutivi è uguale a \(3\), e i cambi sono: \(\,\,+1\,\,\) e \(\,\,-1\,\,\), \(\,\,-1\,\,\) e \(\,\,+1\,\,\), \(\,\,+1\,\,\) e\(\,\,-1\,\,\)

Conclusione: Poiché c'è un cambio di segno tra i coefficienti di \(p(x)\), concludiamo che c'è esattamente UNO zero positivo per \(p(x) = x^4+x^3+x^2-1\).

In base al numero di cambi di segno trovati, che è \(3\), concludiamo che \(p(x) = x^4+x^3+x^2-1\) può avere 1 o 3 radici negative.

Esempio: segni positivi e negativi

Indicare il possibile numero di radici positive e negative di \(x^4 + 1\). Puoi dire qualcosa il numero preciso di radici positive e negative?

Soluzione: In questo caso non ci sono cambi di segno quindi non ci sono radici positive. Ora, \(p(-x) = (-x)^4 + 1 = x^4 + 1\), che non ha cambi di segno, quindi non ci sono nemmeno radici negative. La conclusione è che il polinomio non ha radici reali (poiché nemmeno 0 è una radice).

Altri calcolatori polinomiali

Trovare radici polinomiali è uno dei punti centrali per la maggior parte dei problemi applicativi in Calculus e Algebra, ed è un'abilità che vale la pena padroneggiare.

Ci sono molte abilità coinvolte nel calcolo degli zeri di un polinomio, e Regola Dei Segni Di Cartesio ti dà molte informazioni che possono essere dedotte semplicemente guardando i coefficienti del polinomio.